Abstract: Im vorliegenden Beitrag wird ein qualitativ-rekonstruktiver Zugang für die Analyse von schulischen Unterrichtsinteraktionen beim inklusiven Lernen von Mathematik vorgestellt. Der Schwerpunkt liegt hierbei auf dem Verfahren der Interaktionsanalyse, welches sich im Bereich interaktionistischer Ansätze der Interpretativen Unterrichtsforschung der Mathematikdidaktik etabliert hat. Neben einer methodologischen Verortung und hieraus abzuleitender lerntheoretischer Grundüberlegungen beinhaltet der Beitrag beispielhafte Analysen von Unterrichtsgesprächen, die auf der theoretischen Basis der Entwicklung des Bildes von Mathematik und dem Lernen von Mathematik in der nationalen und internationalen mathematikdidaktischen Forschung das sprachbezogene mathematische Lernen im inklusiven Grundschulmathematikunterricht in den Blick nehmen.
Stichworte: Interpretative Unterrichtsforschung, Interaktionsanalyse, Sprache und Mathematik, Grundschulmathematikunterricht
Inhaltsverzeichnis
Obwohl es mittlerweile eine recht umfangreiche Fülle an Literatur zu qualitativen Forschungsmethoden gibt, scheinen spezifisch fachdidaktisch orientierte Ansätze als ein Teilgebiet empirischer Sozialforschung eher die Ausnahme zu sein. Die geringe Repräsentanz fachdidaktischer qualitativer Forschung, ihrer methodologischen Verortung und ihres methodischen Vorgehens zeigt eine Problematik qualitativer Verfahren in der Unterrichtsforschung bzw. Lehr-Lern-Forschung auf. Die gängige Methodenliteratur scheint vorwiegend orientiert an den Fragestellungen aus der Soziologie und Sozialpsychologie. Diese lassen sich jedoch nicht ohne Weiteres auf fachdidaktische Fragestellungen übertragen, denn wesentliches Merkmal des in der Fachdidaktik gemeinhin untersuchten Gegenstandsbereiches ist das Unterrichten und Lernen von fachlichen (Unterrichts-)Inhalten. Qualitative Methoden in der Fachdidaktik sollten deshalb die spezifische Fokussierung auf fachliche Lerninhalte als konstitutives Element ihrer Analyseverfahren berücksichtigen (vgl. Krummheuer, Schreiber & Schütte 2015).
Nach Meuser (2006) besteht eine grundlegende Gemeinsamkeit einer Vielzahl qualitativer Verfahren der empirischen Sozialforschung darin, dass sie sich an einer rekonstruktiven Methodologie orientieren. Wesentliche Merkmale dieser Verfahren sind, dass man mit ihnen interpretierend und rekonstruierend arbeitet. Hiernach wird die Forschung auch als „interpretative Forschung“ (Wilson 1970) oder „rekonstruktive Forschung“ (Bohnsack 2007) bezeichnet. Rekonstruktives Vorgehen im Sinne von Bohnsack (2007) bedeutet, dass die Wirklichkeit durch die Individuen konstruiert wird und versucht wird, diese Konstruktionen mit rekonstruktiven Verfahren der Interpretativen Forschung zu rekonstruieren. Hiernach sind die theoretischen oder gedanklichen Gegenstände, die von den Forschenden gebildet werden, Konstruktionen der Konstruktionen, die die handelnden Subjekte im Sozialfeld selbst tätigen:
„Die Besonderheit sozialwissenschaftlichen Denkens besteht also darin, dass sich nicht nur dieses Denken selbst aus Interpretationen, Typenbildungen, Konstruktionen zusammensetzt, sondern dass bereits der Gegenstand dieses Denkens, eben das soziale Handeln, das Alltagshandeln auf unterschiedlichen Ebenen durch sinnhafte Konstruktionen, durch Typenbildungen und Methoden vorstrukturiert ist“ (Bohnsack 2007, S. 23).
Im Bereich der mathematikdidaktischen Forschung, welche im vorliegenden Artikel als exemplarischer Gegenstand fachdidaktischer Forschung betrachtet werden soll, lassen sich unter der Bezeichnung Interpretative (Unterrichts-)Forschung[1] rekonstruktiv-interpretative Verfahren der Lehr-Lern-Forschung zusammenfassen. Im vorliegenden Beitrag soll ein Forschen nach dem mathematikdidaktischen Ansatz der Interpretativen Forschung theoretisch aufgearbeitet und am Beispiel illustriert werden. Wir verstehen dabei den mathematikdidaktischen Zugang als ein Beispiel fachdidaktischer Lehr-Lern-Forschung, der sich auch auf andere fachdidaktische Forschungsbemühungen mit geeigneten Adaptionen übertragen ließe.
Interpretative Forschung stellt eine Art Sammelbegriff dar, der sich auf den Untersuchungsgegenstand und den methodischen Ansatz von Forschung bezieht. Zugleich impliziert er einen theoretischen Standpunkt (vgl. Krummheuer & Naujok 1999). Die Interpretative Forschung in der Mathematikdidaktik hat in Deutschland ihren Ursprung Anfang der 1980er Jahre. Ihr Forschungsfokus liegt nicht auf dem Gegenstand einer als statisch und fest aufgefassten Mathematik im Unterricht, sondern auf den erst im alltäglichen Unterricht ständig neu erzeugten Deutungen und Deutungszuschreibungen in der Interaktion der Beteiligten. Im Unterricht werden, diesem Gedankengang folgend, durch die Beteiligten Bedeutungen ausgehandelt, wodurch mathematische situationsüberdauernde Bedeutungszuschreibungen konstruiert werden. Den Schwerpunkt setzt dieser Forschungszweig auf die Analyse der interaktiven Wechselbeziehungen unter den Lernenden selbst (s. z.B. Naujok 2000, Schreiber 2010), zwischen den Lernenden und der Lehrenden (s. z.B. Jungwirth 1991, Schütte 2009) und auf die Kombination aus beidem, d.h. der Wechselbeziehung aller Beteiligten des Unterrichts (s. z.B. Bauersfeld 1978, Brandt 2004, Fetzer 2007, Krummheuer & Brandt 2001, Voigt 1984). In neueren Ansätzen wird der Fokus dieses Ansatzes von der Schule erweitert auf alltägliches Lernen im Kindergarten und in der Familie (vgl. z.B. Brandt, Vogel & Krummheuer 2011, Tiedemann 2012, Schütte 2014).
Übergreifendes Ziel der Interpretativen Forschung ist es, durch das ‚Verstehen‘ von Handlungen von Individuen in konkreter Lehr-Lern-Praxis lokale Theoriegenese zu betreiben. Es stellt sich die Frage, in welchem Verhältnis der Untersuchungsgegenstand ‚alltägliche Unterrichtsinteraktionen im Grundschulmathematikunterricht‘ zur bestehenden oder zur zu entwickelnden Theorie steht. Brandt und Krummheuer (1998) sprechen im Zusammenhang vom Verhältnis von Gegenstand und Theorie der Interpretativen Forschung von der „Unausweichlichkeit von Theoriekonstruktion“ (S. 22) und führen dies auf das Potenzial der permanenten Veränderung von Unterrichtsalltag zurück. Naujok (2000) schränkt den Geltungsbereich des Begriffes Theorie jedoch ein, da dieser in vielen anderen Bereichen meist global und universalistisch konnotiert ist. Die theoretischen Ergebnisse von Forschungen eines rekonstruktiv-interpretativen Vorgehens verfolgen nicht den Anspruch der Entwicklung globalisierender und universalistischer Theorieansätze (vgl. Krummheuer & Naujok 1999). Nach Naujok sind die generierten theoretischen Produkte der Interpretativen Forschung „ eher als Versuche zu betrachten, die empirischen Phänomene und Zusammenhänge zwischen diesen zu erklären“ (S. 32). Nach Kelle (1994) unterscheiden Merton (1968) und Blumer (1954, 1940) bei der Auseinandersetzung mit der hierarchischen Struktur sozialwissenschaftlicher Theorien und der heuristischen Bedeutung von leitenden Annahmen zwischen zwei allgemeinen heuristischen Konzepten: Die einen besitzen eine große Reichweite, aber geringen empirischen Gehalt und hierdurch eine geringe Präzision[2], die anderen lassen sich lediglich auf einen begrenzten sozialen Wirklichkeitsbereich anwenden, stellen aber präzisere und gehaltvollere theoretische Konzepte dar.[3] Die Hypothesen Interpretativen Forschens bleiben demnach der Tatsache verhaftet, dass sie sich auf den jeweiligen Kontext des untersuchten Forschungsfeldes beziehen und somit empirisch gehaltvolle Elemente enthalten und innere Konsistenz aufweisen. Ziel Interpretativer Forschung ist es hierbei anfangs, Ergebnishypothesen zu formulieren, die auf empirischen Befunden beruhen und sich anhand dieser verstehen lassen. Diese empirisch gegründeten und theoretisch fundierten Ergebnishypothesen münden in weiteren Schritten, wie denen der Komparativen Analyse in eine lokale Theorie.
Im vorliegenden Artikel liegt der Schwerpunkt auf den rekonstruktiv-interpretativen Analysen von Unterrichtsgesprächen im inklusiven Mathematikunterricht – also der Verbindung von fachlichem und inklusivem Lernen. Da dieses Forschungsfeld in der deutschsprachigen Forschung nahezu unerforscht ist und der vorliegende Beitrag als ein Versuch einer ersten empirisch gegründeten Annäherung an dieses Feld zu werten ist, wird es uns im Weiteren nicht möglich sein eine lokale Theorie inklusiven Mathematiklernens zu entwerfen, sondern lediglich erste Hypothesen innerhalb von Theoriereflexionen zu den zusammenfassenden Analysen zu generieren, die in weiteren Schritten in eine solche Theorie integriert werden könnten. Insofern vermag der vorliegende Beitrag zwar das Vorgehen der Theorieentwicklung in der Interpretativen Forschung theoretisch herzuleiten. Dem Anspruch dieses empirisch zu belegen, kann und wird der vorliegende Artikel noch nicht zufriedenstellend nachkommen können (zum ausführlichen Vorgehen der Theorieentwicklung siehe Schütte 2009).
Angelehnt an Blumer (1954, 1940) bedarf es für die Konstruktion von Theorien eines theoretischen Vorwissens in Form sensibilisierender und empirisch gehaltvoller Begriffe. Nach Kelle (1994) weisen sensibilisierende Begriffe den Forschenden den Weg zu ihrem Gegenstandsbereich, wo diese dann die jeweilige Ausprägung der Begriffe entwickeln können. Kelle und Kluge (1999) sprechen in diesem Zusammenhang vom „theoretischen Skelett“ (S. 35) sozialwissenschaftlicher Theorien. Krummheuer und Brandt (2001) schreiben, dass sie sensibilisierende Begriffe nahezu wie Begriffe in einer „mathematischen Axiomatik“ (S. 12) benutzen. Sie werden als gegeben vorausgesetzt und stehen für eine empirische Überprüfung auf ihre Stichhaltigkeit nicht zur Disposition. Strauss und Corbin (1996) führen den Gedanken zur theoretischen Sensibilität in der qualitativen Forschung weiter aus und betonen, dass die theoretische Sensibilität es den Forschenden erlaubt, eine Theorie zu entwickeln, die gegenstandsverankert, konzeptuell dicht und gut integriert ist. Dieser Prozess sei überdies schneller, als wenn die Forschenden ihn ohne diese Sensibilität unternommen hätten, denn durch sensibilisierende Begriffe ist es möglich, für die eigene Theorie Grundannahmen zu formulieren, die erzielten Forschungsergebnisse mit den zuvor aufgestellten Grundannahmen zu vergleichen und eigene, neu entwickelte Theorieelemente in bestehende Theorien einzuordnen, d.h., „[...] offene und begrifflich unscharfe soziologische Begriffe sollen als sensibilisierende Konzepte verwendet werden, die durch einen Kontakt mit dem untersuchten Gegenstandsbereich zu definitiven, d.h. empirisch gehaltvollen theoretischen Konstrukten ausformuliert werden“ (Kelle 1994, S. 242).
Nach Kelle (1994) hat sich die Diskussion der Theoriekonstruktion nach der induktiven und deduktiven Schlusslogik in eine erkenntnistheoretische Sackgasse manövriert. Einen Weg aus dieser Sackgasse heraus bietet, so Kelle (1994), die Forschungslogik des hypothetischen Schließens, die auf Peirce (1991) zurückgeht. Sie wird in der qualitativen Unterrichtsforschung und vor allem in der Interpretativen Forschung angewendet. Unter die Forschungslogik des hypothetischen Schließens fallen die von Peirce entwickelten Schlussmodi der qualitativen Induktion und Abduktion. Werden beim hypothetischen Schließen empirische Phänomene als Fälle von bekannten Regeln bzw. Theorien erklärt, fällt diese Art der Theorieentwicklung in den Bereich der qualitativen Induktion. Hierbei werden keine neuen Erklärungen konstruiert, sondern zur Erklärung empirischer Phänomene als gesichert geltende Erkenntnisse herangezogen. Eine solche Schlusslogik wird in der vorliegenden Untersuchung angewendet, wenn die Ergebnisse der Analysen vor dem Hintergrund bereits bestehender theoretischer Ansätze zum sprachlichen Lernen im Mathematikunterricht gedeutet werden.
Diese Art des Schließens ist häufig jedoch nicht möglich, wenn die bestehende Theorie Phänomene der Empirie nicht zu beschreiben oder erklären vermag oder mit bestehenden Theorieansätzen widersprüchliche Interpretationen von beobachteten Fällen auftreten, so dass sie geändert oder neu generiert werden muss, damit die empirischen Phänomene erklärbar werden. In diesem Sinne stellt das ‚Versagen‘ der qualitativen Induktion den Beginn von Theorieentwicklung dar. Es bedarf einer weiteren Schlussform, der Abduktion. Fraglos akzeptierte Annahmen, welche als Grundlage der qualitativen Induktion dienten, werden zur Disposition gestellt und die durch das bis dato geltende theoretische Wissen abgesteckten Grenzen überschritten (vgl. Kelle 1994, Naujok 2000). Das Ergebnis des Schlussvorgangs einer Abduktion stellt die Hypothese dar. Kelle (1994) schreibt hierzu: „Die Formulierung neuer Hypothesen auf der Basis empirischen Materials beruht nicht auf dem Induktionsprinzip, sondern auf dem von Charles Peirce formulierten Modell des hypothetischen Schließens, in welchem der deduktive Schlussmodus, der in experimentellen Methodologien Anwendung findet, quasi ‚umgedreht‘ wird: es wird nicht die Existenz eines empirischen Phänomens mit Hilfe einer Hypothese postuliert, die aus einer vorhandenen Theorie deduziert wurde, um diese Theorie zu überprüfen; vielmehr wird eine Erklärung für ein neu entdecktes empirisches Phänomen gesucht.“ (S. 355). In der Peirce’schen Terminologie stellen abduktive Schlussformen somit den eigentlichen generativen Aspekt von Theorieentwicklung dar, bei dem Theorie aus dem Gegenstand selbst entwickelt wird (vgl. Peirce 1991). Krummheuer und Brandt 2001 führen jedoch aus, dass die Abduktion „[...] im Vergleich zur Induktion und Deduktion [...] ein relativ schwacher Schluss“ ist (S. 80), denn zu einem überraschenden Phänomen lassen sich immer eine Vielzahl neuer Regeln oder Theorieelemente konstruieren, so dass das Phänomen ein Fall dieser Regeln oder dieser Theorieelemente ist (vgl. Brandt 2004). Allerdings ist nach Peirce (1991) „[...] jedes einzelne Stück wissenschaftlicher Theorie, das heute festgegründet dasteht, [...] der Abduktion [zu] verdanken“ (S. 172). Dies unterstreicht den vorerst hypothetischen Charakter der durch Abduktion gewonnenen neuen Regeln und Theorieelemente, jedoch auch ihre Bedeutung bei der Konstruktion von Theorieelementen. Die Abduktion stellt die Forscherin oder den Forscher jedoch auch vor das Problem, dass sie kein Prinzip darstellt, das es erlaubt, mit Hilfe methodischer Konzepte oder Regeln in einem Forschungsablauf Schlussfolgerungen zu ziehen. Das Vorgehen der Theoriekonstruktion einer abduktiven Schlusslogik ist letztlich nicht methodisierbar (vgl. Kelle 1994, Naujok 2000).
Wie lässt sich der Geltungsbereich von Ergebnissen der Interpretativen Forschung jedoch vom Status reiner Fallanalysen auf eine größere Generalisierbarkeit im Sinne abduktiv gewonnener Hypothesen übertragen, wenn das Vorgehen der Abduktion letztlich nicht methodisierbar ist? Es bedarf bei einem abduktiven Vorgehen der Entwicklung eines „Forschungsstils“ (Bohnsack 2007, S. 198), der Abduktionen begünstigt. Hierzu lässt sich auf ein zentrales Element des Forschungsstils der Grounded Theory, die komparative Analyse – „constant comparative method“ (Glaser & Strauss 1967, S. 101 ff.; Strauss & Corbin 1994, S. 273) – verweisen. Die komparative Analyse ist eine Methode der Vergleichsgruppenbildung, die auf allen Ebenen des Forschungsprozesses anzuwenden ist und Abduktionen begünstigt. Sie bezeichnet nicht nur einen bestimmten Analyseschritt innerhalb des Forschungsprozesses, sondern fungiert als den ganzen Forschungsprozess bestimmender methodischer Ansatz. Anfangs ist es bei der komparativen Analyse das Ziel, das Spezielle an einem Realitätsausschnitt darzustellen, danach wird über eine geeignete theoretische Auswahl die Spezifität der jeweiligen Fälle in ihrer Relation zueinander untersucht. Durch Komparationen lässt sich die Kritik aus der deduktiv-nomologischen Forschungsrichtung, dass die erzielten Ergebnisse qualitativer Arbeiten nur für einzelne Fälle Gültigkeit und somit kaum Relevanz besäßen, entkräften. Komparationen heben die Analysen der Untersuchung über einen Status von Fallanalysen hinaus. Der Vergleich der Fälle untereinander bringt Dimensionen hervor, die bei reiner Betrachtung der Fälle nicht zur Geltung kommen würden. So ergibt sich durch Komparationen ein erweiterter ‚Denkraum‘, in dem man nach Lösungen suchen oder mögliche Theorieelemente generieren kann.
Mit der Verortung in einem rekonstruktiv-interpretativen Verfahren der Interpretativen Forschung scheint es im Folgenden notwendig, nicht nur den theoretischen Rahmen der Untersuchung in Bezug auf inklusives Mathematiklernen zum Aufbau des theoretische Skelets herzuleiten, sondern ebenso die lerntheoretischen Grundüberlegungen des interpretativen Zugangs darzustellen. Ein Forschungsansatz, der der Interpretativen Logik folgt, führt unweigerlich zu einem besonderen Blick auf die Welt und auf das Lernen im Fach.
Das Bild vom Lernen von Mathematik hat sich in den letzten gut 30 Jahren in der internationalen und nationalen mathematikdidaktischen Forschung vehement verändert. Fokussierte die internationale sowie die nationale Mathematik der Grundschule zum Ende der 1970er Jahre vor allem auf das Erlernen von Fertigkeiten und isolierten mathematischen Begriffen einer ‚fertigen Mathematik’ mit dem Schwerpunkt im arithmetischen Bereich, vollzog sich gegen Mitte der 1980er Jahre ein Wandel. Als Ergebnis dieser Entwicklung lassen sich die vorgeschlagenen Reformen des amerikanischen National Council of Teachers of Mathematics (NCTM) in den „Curriculum and Evaluation Standards for School Mathematics“ im Jahre 1989 verstehen. Parallel dazu – zu einem großen Teil sicherlich auch ausgehend von diesen Reformen – entwickelte sich in der internationalen mathematikdidaktischen Community ein neues Verständnis vom Lernen von Mathematik. Nach diesem sollten Kinder in der Schule künftig nicht nur mathematische Fertigkeiten erlangen, sondern auch die mathematischen Konzepte dahinter entdecken und verstehen, über diese mit der Lehrperson und den Mitlernenden kommunizieren und argumentieren, um so schlussendlich selbstständig Begründungen für mathematisches Handeln hervorbringen zu können (vgl. Boyd & Bargerhuff 2009, Collins 1994, Kroesbergen, Van Luit & Maas 2004, NCTM 1989). Diese internationale Entwicklung führte auch in Deutschland zu einem veränderten Bild von Mathematik der (Grund)Schule. Mathematik galt nunmehr international wie national als eine kulturell überlieferte, durch Sprache (vgl. D’ Ambrosio 1985, Schütte 2009, Schütte & Kaiser 2011) vermittelte und konstruierte Kulturtechnik. Kinder und Erwachsene sollen hiernach in die Lage versetzt werden, die Welt besser zu verstehen und über das Entdecken von Zusammenhängen, Mustern und Strukturen zudem auch die Schönheit der Mathematik zu erfahren. Diese Veränderung wurde in Deutschland über die Festschreibung der Bildungsstandards im Fach Mathematik für den Primarbereich der Kultusministerkonferenz im Jahre 2004 für die Grundschule verbindlich institutionalisiert. Mit der Einführung der Bildungsstandards wurde hierbei nicht nur die Breite der mathematischen Inhalte der Grundschule über die Arithmetik und die Geometrie hin zu Themen, wie z.B. dem der Stochastik geöffnet, es wurden auch explizit ‚nicht-inhaltsbezogene’, sogenannte prozessbezogene Kompetenzen festgeschrieben, wie die des Argumentierens, des Problemlösens, des Modellierens, des Darstellens und des Kommunizierens (vgl. Ständige Konferenz der Kultusminister 2005).
Mit diesem veränderten Bild und den Erkenntnissen aus der aktuellen Unterrichtsforschung wurde auch das vorherrschende Verständnis von Lernen von Mathematik selbst in Frage gestellt. Bis zu Beginn 1980er Jahre fußte der nationale und internationale Mathematikunterricht auf einem behavioristischem Verständnis von Lernen, welches sich durch einen kleinschrittigen systematischen Aufbau der mathematischen Lerninhalte auszeichnete, die von Außen in wohl überlegter Art und Weise durch verschiedenste Formen der ‚Belehrung’ an das zu lernende Individuum herangetragen wurden. Aus der Sicht des Lernenden bedeutete dies ein vorwiegend passives rezeptives Lernen, welches durch gezielte externe Reize von Außen gesteuert wurde. Seit Mitte der 1980er Jahre wurde dieses Bild zunehmend durch konstruktivistisch geprägte Ansätze des Lernens von Mathematik verdrängt. Hiernach veränderte sich die Aufgabe der Lehrenden vor allem dahingehend, die Bedingungen des aktiven Mathematiklernens von Kindern zu verbessern (vgl. Boyd & Bargerhuff 2009, Krauthausen & Scherer 2007, Winter 1991).
In dem Zusammenhang eines veränderten Bildes vom Lernen von Mathematik lassen sich über die letzten drei Jahrzehnte relativ stabil zwei theoretische Positionen in der deutschsprachigen Mathematikdidaktik identifizieren, die sich von behavioristisch geprägten Lerntheorien distanzieren jedoch über ihre theoretischen Grundpositionen als auch auf unterrichtspraktischer Ebene über die Effektivität der je entwickelten Unterrichtsvorschläge streiten. Diese gehen auf der einen Seite auf sozial-konstruktivistisch fundierte Lernansätze und auf der anderen Seite auf Vorstellungen, die sich aus Theorien des kognitiven Konstruktivismus speisen, zurück. In Bezug auf die Differenzierung der beiden grundlegenden Lernansätze kann auf Tobias und Duffy (2009) verwiesen werden. Im Folgenden wird zur Problematisierung dieses Spannungsverhältnisses aus dem Blickwinkel der thematisierten beiden Forschungstraditionen auf das fachgebundene Lernen im Mathematikunterricht geblickt. Zur Schärfung der Problemstellung übernehmen wir die antagonistische Unterscheidung von Miller (1986): Lernen kann entweder als monologischer Prozess im Sinne des Genetischen Individualismus[4] im Individuum verankert oder als dialogischer Prozess im Sinne des Genetischen Interaktionismus[5] zwischen Individuen positioniert verstanden werden.
Dem Genetischen Individualismus zufolge liegen alle entscheidenden Mechanismen zum Lernen in der psychischen Konstitution des Individuums, so dass Mechanismen und Prozesse dieses Lernens auch nur den Individuen zugeschrieben werden können. Zu nennen sind hier in der deutschsprachigen Mathematikdidaktik u. a. Arbeiten von Wittmann und Müller (1990), Wittmann (2002), Hirt und Wälti (2008) sowie Krauthausen und Scherer (2010)[6]. Diese genannten Autoren grenzen sich von einer behavioristisch geprägten Orientierung des Lernens durch Belehrung ab, in welcher der kindliche Geist durch die gezielte Anwendung von Außen durch Wissen ‚angereichert’ werde. Wittmann (1990) schreibt dazu: „In der trockenen Sprache des Behaviorismus ist Lernen nichts anderes als ein relativ stabiler Zuwachs im Verhaltensrepertoire, der das Ergebnis von Übung und dabei erfolgender Bestärkung bzw. Verhaltenskorrektur ist“ (S. 157). Nach behavioristischem Verständnis müsse der Lernende Wittmann (1990) folgend lediglich seine Sinne schärfen und ihm die dargebotenen Reize verarbeiten und imitieren. Eine aktivistische Position des Lernens hingegen gründet sich dieser Forschungstradition folgend vor allem auf der genetischen Psychologie von Piaget. Hiernach entsteht Wissen im Individuum durch einen individuellen Konstruktionsprozess und lässt sich nicht von Außen implementieren. Vor diesem theoretischen Blickwinkel lässt sich die heute gängigere Orientierung des aktiv-endeckenden Lernens verstehen (vgl. Winter 1991), in der Kinder sich einen Unterrichtsgegenstand selbstständig erarbeiten müssen, um mathematische Lernfortschritte zu vollziehen (vgl. u. a. Wittmann 1990). Vertreter dieser Forschungstradition in der Mathematikdidaktik konzentrieren sich zur Veränderung der Bedingungen des Lernens von Mathematik vor allem auf die Entwicklung von Aufgaben oder Lernumgebungen, in denen das Individuum möglichst selbstständig eigenes Wissen konstruieren kann. In diesem Zusammenhang lässt sich auf den vielfach verwendeten Begriff der „substantiellen Lernumgebungen“ (siehe z. B. Krauthausen & Scherer 2010) verweisen. Ein Ziel dieser Lernumgebungen ist es, dass es jungen Lernern mit unterschiedlichen Fähigkeiten und unterschiedlichem Alter ermöglicht wird, zentrale mathematische Inhalte in einer Ganzheitlichkeit zu erfahren, so dass ihnen fundamentale Lernschritte erfahrbar werden. Hierbei sollen die Lernumgebungen oder Aufgabenformate dergestalt sein, dass eine aus dem Material selbst entstehende „natürliche Differenzierung“ (zum Begriff siehe ebenda, S. 5) erreichbar wird und Lernende mit unterschiedlichen Fähigkeiten an denselben Aufgaben arbeiten können. Ziel ist es hierbei, dass der mathematische Inhalt der substantiellen Lernumgebungen einer gewissen ganzheitlichen Offenheit unterliegt und von den Lernenden aus dem Material herausgearbeitet werden soll.
Dieser mathematikdidaktischen Forschungsorientierung stehen Ansätze des Genetischen Interaktionismus gegenüber, die sich mit Fokus auf den interaktiven Wechselbeziehungen im Unterricht von Ansätzen des Genetischen Individualismus und seiner Reduzierung auf die zu vermittelnden mathematisch-stofflichen Inhalte abzugrenzen versuchen. Für die Vertreter des Genetischen Interaktionismus ist Lernen ein dialogischer Prozess, der sich nur im Zuge einer Koordination mentaler Aktivitäten von zumindest zwei Individuen beschreiben lässt. Der Genetische Interaktionismus geht dabei im Gegensatz zum Genetischen Individualismus davon aus, dass nur in der sozialen Gruppe und aufgrund sozialer Interaktionsprozesse zwischen den Individuen dieser Gruppe, dem einzelnen Individuum fundamentale Lernschritte ermöglicht werden können (vgl. Miller 1986, Krummheuer & Fetzer 2005, Schütte 2009). Anhänger des Ansatzes der Interpretativen Forschung der Mathematikdidaktik, der sich im Genetischen Interaktionismus verorten lässt, hatten ursprünglich das Ziel, die Forschung stärker beschreibend auf ein „Verstehen-Wollen“ als vorschreibend auf ein „Verändern-Wollen“ des Mathematikunterrichts zu richten. Es erfolgte eine Abkehr und kritische Abgrenzung von den bis dato gängigen stoffdidaktischen Ansätzen der Unterrichtsforschung, die lediglich versuchten, Unterricht zu verändern, ohne ihn zuvor zu verstehen. Unter dem Paradigma des Genetischen Interaktionismus analysieren u. a. Maier und Voigt (1991), wie im alltäglichen Unterricht Bedingungen für mathematisches Lernen geschaffen werden. Sie arbeiten heraus, wie selbstverständlich es im Mathematikunterricht sei, dass die Lehrperson entwickelnde Fragen stelle, was eher dem Verständnis einer behavioristischen Orientierung zum Lernen entspräche und legen den Ursprung dieser Unterrichtsgestaltung offen – den sokratischen Dialog. Maier und Voigt verweisen darauf, dass der Grundgedanke einer entwickelnden Lehrerfrage in dem Bild einer fertigen und geschlossenen Mathematik liege. Diese müsse nicht in Interaktionen des Unterrichts unter den Individuen ausgehandelt werden, was wie oben bereits dargelegt, nicht dem aktuellen Bild von Mathematik entspräche. Die Entwicklungsfrage böte nach Maier und Voigt den Lernenden die Möglichkeit einen Gedanken, den die Lehrperson in „unvollständiger Form“ geäußert habe zu „ergänzen“ (S. 27) – und dies mit relativ geringem Aufwand sowie einem Mindestmaß an Fehlerrisiko für die Lernenden. Nach Krummheuer (2002; s.a. Bauersfeld 1978) lässt sich der Ursprung eines solchem Unterrichtsgesprächs in dem Anspruch der exakten „Plansollerfüllung“ (ebenda, S. 76) finden. Ein solcher Unterricht widmet sich demnach nicht dem Gedanken der Optimierung der Bedingungen von Lerngelegenheiten. Unvorhersehbare Äußerungen der Schülerinnen und Schüler werden als störend empfunden, aus dem Unterricht verbannt und dieser läuft um so reibungsloser, je mehr routinisierte Elemente in ihm ablaufen (Krummheuer 2002). Mit dem Ausdruck der optimierten Bedingungen der Lernermöglichung soll dabei einem interaktionistischen Gedanken Rechnung getragen werden, der sich ebenfalls vom Reiz-Reaktions-Lernen einer behavioristischen Tradition abgrenzt. Hiernach gilt es die Bedingungen der Möglichkeit des Lernens zu verbessern und nicht die Bedingungen des Lernens, da es dem jeweiligen Individuum selbst überlassen bleibt, in welcher gearteten Form es diese Bedingungen für sich selber nutzt. In diesem Zusammenhang lässt sich auf Bauersfeld (1985, S. 8) verweisen. Dieser konstatiert, dass der Mathematikunterricht sich vielfach als eine „Vermittlungspraxis mathematischen Wissens“ verstehe und, dass innerhalb dieses Verständnisses neben anderen vor allem auch die „interaktiven Wechselbeziehungen“ der Beteiligten vernachlässigt werden.
Verweisen lässt sich in diesem Zusammenhang z. B. auf die Arbeit von Krummheuer und Brandt (2001), die Interaktionsprozesse im Unterricht anhand ihres Potentials zur Lernermöglichung differenzieren. Günstige Bedingungen für Mathematiklernen in unterrichtlichen Interaktionsprozessen bezeichnen sie mit dem Begriff „interaktionale Verdichtung“ weniger günstige mit dem Begriff „interaktionalen Gleichfluss“. Der interaktionale Gleichfluss stellt den Autorinnen und Autoren zufolge eine Minimierung des unterrichtlichen Konfliktpotenzials dar und charakterisiert Interaktionsverläufe, die scheinbar nahezu reibungslos ablaufen (s. a. Bauersfeld 2000). Die Teilnahme am Unterricht erfordert in solchen Interaktionsverläufen wenig Aufmerksamkeit, den Lernenden werden relativ leicht nachvollziehbare Lerngegenstände präsentiert, wodurch die Beteiligten keine argumentativen Konflikte eingehen und keine tieferen Argumentationen hervorbringen. Somit emergieren in dieser Form des Unterrichts Lernermöglichungsbedingungen, die als nicht optimal anzusehen sind. Interaktionale Verdichtungen stellen hingegen Optimierungen von Lernermöglichungsbedingungen dar. Sie sind durch Interaktionsverläufe gekennzeichnet, die eher krisenhaft behaftet sind und weniger reibungslos ablaufen. In interaktionalen Verdichtungen werden relativ umfassende kollektive Argumentationen (zum Begriff siehe Miller 1986; Krummheuer 1992; Krummheuer & Brandt 2001) in musterhaften Interaktionsstrukturen hervorgebracht, in denen es Kindern ermöglicht wird in Form von produktiven oder rezeptiven Partizipationsmöglichkeiten einen Zuwachs an Handlungsautonomie zu erlangen. Der mathematische Unterrichtsalltag scheint sich dabei nicht dauerhaft optimierbar zu zeigen. Es vollzieht sich ein stetiger Wechsel zwischen interaktionalen Verdichtungen und interaktionalem Gleichfluss, wobei letzterer als vorherrschend im alltäglichen Unterricht anzusehen ist (vgl. Krummheuer 2004).
Eine Parallele der unterschiedlichen Ansätze scheint somit der Grundgedanke zu sein, dass zur Ermöglichung von fundamentalen Lernschritten eine gewisse fachliche Offenheit und Ganzheitlichkeit von Problemen unabdingbar scheint. Fokussieren Ansätze, die dem Genetischen Interaktionismus zuzuordnen sind, dabei auf die Veränderung und Optimierung der Bedingung der interaktiven Bedeutungsaushandlung dessen, was im mathematischen Unterricht gerade Gegenstand ist, streben Ansätze, die auf den Genetischen Individualismus zurückgehen, die Veränderung des mathematischen Gegenstandes z.B. von Aufgaben oder Lernumgebungen an denen die Kinder ihre individuellen Konstruktionsversuche und Aushandlungsprozesse vornehmen, an. Das Ergebnis des oben beschriebenen Paradigmenwechsels in der deutschen Grundschulmathematikdidaktik – unter der Berücksichtigung beider Lernansätze – zeigt sich auch in den bereits erwähnten 2004 verabschiedeten Bildungsstandards der Kultusministerkonferenz für das Fach Mathematik für die Primarstufe. So rückt in den jüngst entwickelten Bildungsstandards neben dem Inhalt, gleichberechtigt und explizit – vertreten durch die allgemeinen prozessbezogenen Kompetenzen – das ‚Wie’ des Unterrichtens in den Vordergrund. Zu Beginn der Ausführungen in den Bildungsstandards wird hiernach festgehalten, dass die Entwicklung mathematischer Grundbildung „...[] nicht nur davon ab[hängt], welche Inhalte unterrichtet wurden, sondern in mindestens gleichem Maße davon, wie sie unterrichtet wurden, d. h. in welchem Maße den Kindern Gelegenheit gegeben wurde, selbst Probleme zu lösen, über Mathematik zu kommunizieren usw.. Die allgemeinen mathematischen Kompetenzen sind mit entscheidend für den Aufbau positiver Einstellungen und Grundhaltungen zum Fach. In einem Mathematikunterricht, der diese Kompetenzen in den Mittelpunkt des unterrichtlichen Geschehens rückt, wird es besser gelingen, die Freude an der Mathematik und die Entdeckerhaltung der Kinder zu fördern und weiter auszubauen.“ (Ständige Konferenz der Kultusminister 2005, S.6) Hiermit scheint auch die deutsche Bildungspolitik und -administration ein in der Forschung schon länger vertretenes und geteiltes Bild von Mathematik und möglichen Zugängen zum Lernen einer solchen Mathematik aufgegriffen zu haben.
Im Bereich der Sonderpädagogik der Mathematikdidaktik lassen sich, wenn auch mit Verzögerung eintretend, ebenfalls die oben beschriebenen Veränderungen von einem Verfechten von kleinschrittig-reproduktiven Ansätzen des Mathematiklernens hin zu offeneren Unterrichtskonzepten des aktiv-entdeckenden Lernens erkennen (vgl. für nationale Mathematikdidaktik u. a. Scherer 1995; Ratz 2009). Im Zusammenhang von Mathematikunterricht für Kinder mit sonderpädagogischen Förderbedarf wurden und werden diese Veränderungen allerdings kontrovers diskutiert. Sie stehen in diesem Bereich der (bewährten) behavioristischen Unterrichtstradition, die geprägt ist durch eine Reduktion der Lerninhalte, eine Isolierung von Schwierigkeiten und ein kleinschrittiges Vorgehen mit fest vorgegeben Lösungswegen (vgl. Boyd & Bargerhuff 2009; Moser-Opitz, Stöckli, Pfister & Leuser 2014). Diese Tradition wird durch Ergebnisse von internationalen Studien und Meta-Studien bestärkt, die die positiven Effekte einer strukturierten Wissensvermittlung, die auf gezielter Anleitung beruht, für den Unterricht von Kinder mit sonderpädagogischen Förderbedarf empirisch begründen und somit Zweifel an einem offenen auf aktiv-entdeckend ausgerichteten Mathematikunterricht als geeigneten Zugang zur Wissensvermittlung für Kinder mit sonderpädagogischen Förderbedarf aufkommen lassen (vgl. u. a. Kroesbergen, Van Luit & Maas 2004; Gersten, Chard, Jayanthi, Baker, Morphy & Flojo 2009). Auf der andere Seiten finden sich durchaus Forschungsergebnisse, die positive Effekte der Umsetzung des aktiv-entdeckenden Lernens im Mathematikunterricht mit Kindern mit sonderpädagogischen Förderbedarf aufzeigen (vgl. Scherer 1995; Ratz 2009; Cawley 2002). Letztendlich rückt in diesem Zusammenhang die Frage ins Zentrum, was als Ziel des Mathematikunterrichts für Kinder mit sonderpädagogischen Förderbedarf formuliert wird: Ist die Vermittlung von Fertigkeiten für das Beherrschen von Rechnungen, um einen reibungsloseren Alltag mit ausreichend Grundfertigkeiten zu bestehen das Ziel des Unterrichts? Oder ist es das Ziel, ein tiefergehendes Verständnis der Mathematik zu erreichen und diese als Wissenschaft von Mustern und Strukturen zu verstehen, welche die Welt zu erklären vermag und über die man mit anderen in den in Austausch treten kann? Letzteres würde dem Bild von Mathematik entsprechen, welches wir als Grundlage für das Lernen von Mathematik für Kinder ohne sonderpädagogischen Förderbedarf zurate ziehen.
Im Zuge der Umsetzung des Artikels 24 der UN-Konvention über die Rechte von Menschen mit Behinderung, dem Recht auf ein integratives Bildungssystem ohne Diskriminierung, wird mittlerweile in nahezu allen Bundesländern ein inklusiver (Mathematik-)Unterricht in der Grundschule, in dem alle Kinder gemeinsam Lernen angeboten. Hierbei sollen alle Kinder ungeachtet von Beeinträchtigungen, Herkunft, Geschlecht etc. die Möglichkeit zur sozialen und fachlichen Teilhabe an mathematischen Lernprozessen gegeben werden. Berücksichtig man die oben ausgeführten Überlegungen zum Lernen von Mathematik und die aktuellen Bildungsstandards, so bedeutet dies, das der Mathematikunterricht allen Kindern und eben auch denen mit sonderpädagogischem Förderbedarf Gelegenheiten bieten muss, nicht nur (Rechen-)Fertigkeiten zu trainieren sondern Mathematik als eine Wissenschaft kennenzulernen, die ihnen hilft, die Welt besser zu verstehen und über das Entdecken von Zusammenhängen, Mustern und Strukturen auch die Schönheit der Mathematik zu erfahren. Wollring (2015, S. 37) weist überdies auf den wichtigen Aspekt der Teilhabe an der Kultur des kollektiven Mathematiktreibens in der Schule hin und vertritt die Meinung, dass Teilhabe am Mathematikunterricht nicht nur Teilhabe am Unterrichtsgeschehen bedeuten sollte, sondern im Rahmen von Kooperationen mit Mitschülern und Mitschülerinnen auch „Teilhabe am Zustandebringen von Problemlösungen“. Diese Bedeutsamkeit der Interaktion und sprachlichen Aushandlung für das Lernen von Mathematik zeigt sich auch in Forschungsergebnissen, die vor allem die Verbalisierung von Lernprozessen als förderliche Komponente des Mathematiklernens hervorheben (vgl. u. a. Gersten et al. 2009). Ohne diesen Anspruch an inklusive Lernsettings scheint der Gedanke einer fachlichen Teilhabe aller am Unterricht eine Utopie, was schlussendlich in einer Institution, die vordergründig als Bildungsinstitution angelegt ist, auch den Verlust der sozialen Teilhabe nach sich ziehen würde.
Erste fachdidaktische Ansätze, die sich mit dem Lernen von Mathematik in inklusiven Klassen beschäftigen, greifen hierzu meist das Konzept der natürlichen Differenzierung bzw. das der substantiellen Lernumgebungen (vgl. Wittmann 2010; Krauthausen & Scherer 2010) auf und arbeiten auf dieser Grundlage Lernumgebungen für einen inklusiven Mathematikunterricht aus (vgl. Häsel-Weide & Nührenbörger 2015). Auch in diesen Ansätzen mit dem Fokus auf der Entwicklung optimierter mathematischer Lernumgebungen wird wiederholt betont, dass aus fachlicher Perspektive der Austausch über Vorgehensweisen und Vorstellungen und damit die Kooperation und Interaktion in der Lerngruppe von zentraler Bedeutung sind (vgl. Häsel-Weide & Nührenbörger 2015, S. 61). Krauthausen und Scherer (2010) konstatieren, mit Verweis auf Lorenz (2000), dass eine zunehmende Heterogenität in den deutschen Grundschulklassen unwiderruflich feststehe und bei einer gleichzeitigen Öffnung der inhaltlichen Auseinandersetzung sowohl die sprachliche Gestaltung während als auch die sprachliche Reflexion am Ende der offenen eigenen aktiv-entdeckenden Konstruktionsphasen eine besondere Bedeutung erlange. So würden sich Aufgabenlösungen von Schülerinnen und Schülern, so Krauthausen und Scherer (2010b), aufgrund der zunehmenden Heterogenität der Schülerschaft deutlich unterscheiden. Hierdurch erlangt die sprachlich angeleitete Plenumsphase durch die Lehrperson eine große Bedeutung im Finden von gemeinsamen mathematischen Strukturen in den unterschiedlichen Zugängen der Schülerinnen und Schüler. Korff (2015, S. 103) folgert, dass „im Zentrum eines inklusiven Mathematikunterricht [...] sowohl aus mathematikdidaktischer als auch aus inklusionspädagogischer Perspektive Kommunikation und Kooperation stehen [muss].“ Auch Tiedemann (2015) unterstreicht diese Bedeutung der Sprache in einem inklusiven Mathematikunterricht. In diesem sind Schüler und Schülerinnen ihr zufolge mit sehr unterschiedlichen Fähigkeiten gefordert, Äußerungen von Lehrenden und Mitlernenden verstehend zu verfolgen und sich selbst sprachlich auszudrücken (vgl. ebenda). Diese sehr verschiedenen Voraussetzungen der Lernenden haben demnach großen Einfluss auf die Teilhabe aller an den kollektiven Argumentationen des Unterrichts. Korff (2015) führt hierzu allerdings auch einschränkend aus, dass Lehrkräfte, die in inklusiven Settings unterrichten, der Vielfalt der Schüler und Schülerinnen aktuell überwiegend mit dem Einsatz von individualisierten Arbeitsmaterialien in Stationen- oder Wochenplanarbeit begegnen und Situationen des gemeinsamen Lernens in Erarbeitungs- oder Reflexionsphasen nur äußerst selten stattfinden (vgl. auch Moser-Opitz, Stöckli, Pfister & Leuser 2014).
In Bezug darauf, wie Lehrpersonen diesen aus inklusiven Lernsettings entspringenden (sprachlichen) Anforderungen begegnen können, lassen sich folgende Grundideen beider lerntheoretischen Grundansätze herausfiltern. Aus der Perspektive des Genetischen Interaktionismus unterliegen unterrichtliche Aushandlungsprozesse der Beteiligten aufgrund der Unmöglichkeit ihrer detaillierten inhaltlichen Vorabplanbarkeit einer nach vorn gerichteten Offenheit. Somit müssen Lehrpersonen über eine situationsbezogene Interpretationskompetenz verfügen, um z.B. auf die nicht planbaren Möglichkeiten zu Interaktionalen Verdichtungen mit „ad-hoc Entscheidungen“ (Krummheuer & Brandt 2001) adäquat in der Situation zu reagieren. Unter kognitiv-konstruktivistischer Perspektive in der Tradition des Genetischen Individualismus hingegen sollte die Lehrperson gerüstet sein, die individuellen mathematischen Konstruktionen von Schülern und Schülerinnen sprachlich zu unterstützen und darüber hinaus über Plenumsphasen auch der gesamten Klasse zugänglich zu machen, so dass alle Kinder an den individuellen Entdeckungen der Mitlernenden profitieren können. Gemeinsam scheint beiden Grundorientierungen, dass sie auf mathematische Entdeckungen im Unterricht setzen und für diese im Hinblick auf die zunehmende Heterogenisierung der Lerngruppen eine gesteigerte Bedeutung der Unterstützung der sprachlichen Aushandlung bzw. der Begleitung und Initiierung von mathematischen Interaktionsprozessen durch die Lehrpersonen ausmachen.
Es sind nach obigen Ausführungen erste Bemühungen aus der mathematikdidaktischen Forschung erkennbar, auch in inklusiven Lehr-Lernsettings einen Mathematikunterricht der (Grund-)Schule zu gestalten, der sich an dem neuen Bild von Mathematik orientiert. Dies jedoch vordergründig von mathematikdidaktischen Ansätzen ausgehend, die sich der Perspektive des Genetischen Individualismus zuordnen lassen und den Fokus auf die Veränderung des Gegenstandes der Mathematik – den mathematischen Inhalten hier Lernumgebungen – legen. Es gibt hingegen auch aktuell starke Strömungen aus der Sonderpädagogik, die für Kinder mit sonderpädagogischem Förderbedarf auf ein klassisches Bild von Mathematik und einer eher kleinschrittigen Vermittlung von Fertigkeiten setzen. Insofern versucht der vorliegende Artikel erste Bemühungen zu unternehmen aus Sicht interaktionistischer Ansätze der Interpretativen Unterrichtsforschung Mathematiklernen unter den Bedingungen von Inklusion zu beschreiben und hierbei Unterricht zu untersuchen, der sich auf die unterschiedlichen Zugänge zum Lernen von Mathematik bezieht. Dies aus dem Grundverständnis, dass inklusive Lernbedingungen zu einem nicht unerheblichen Teil vor allem Einfluss auf die interaktiven Wechselbeziehungen zwischen der Lehrperson und den Lernenden sowie zwischen den Lernenden selbst haben werden. Vor allem im Unterricht der Grundschule, wo sehr junge Schülerinnen und Schüler aufeinander treffen, laufen Miller (1986) folgend Lernprozesse vorwiegend kollektiv und dialogisch ab, wonach dort dem autonomen individuellen Lernen eine eher geringe Bedeutung beizumessen ist und interaktionistischen Ansätzen des Lernens und eine größeren Bedeutung beigemessen werden kann.
Kinder benötigen nach obigen Ansätzen fachspezifische sprachliche Fähigkeiten, die es ihnen ermöglichen an einem sprachlich geführten Fachdiskurs sozial und fachlich teilhaben zu können und in Form von kollektiven Argumentationen durch Sprache mathematische Bedeutungen auszuhandeln. Die Aufgabe der Lehrperson besteht demnach einerseits zunächst einmal darin Sprachanlässe im Mathematikunterricht zu initiieren, die es den Schüler und Schülerinnen ermöglichen mathematisch zu kommunizieren und argumentieren und andererseits darin ihnen Hilfestellungen anzubieten an der Interaktion im Unterricht ihren Fähigkeiten entsprechend aktiv teilzunehmen. Für beides bedarf es als Grundlage eines sprachlichen Vorbildes durch die Lehrperson an dem die Lernenden in Form der Zunahme von Handlungsautonomie beim fachbezogenen sprachlichen Handeln wachsen können. Ergebnisse von Untersuchungen zur Lehrerkommunikation in inklusiven Mathematikstunden, wie die der Untersuchung von Wiebe Berry und Kim (2008) weisen allerdings darauf hin, dass die gängige Interaktion in inklusiven Unterrichtssettings vor allem durch eine enge Unterrichtsführung mit wenig Sprach- bzw. mathematischen Argumentationsanlässen für die Schüler und Schülerinnen bestimmt ist. Von den Lehrkräften werden vorwiegend Fragen gestellt, deren Antworten als bekannt vorausgesetzt werden, welche das typische Format des Lehrervortrags unterstützen (vgl. Wiebe Berry & Kim 2008). Diese meist sehr kleinschrittigen Fragen, haben den Vorteil, dass viele Kinder - ohne Fehler zu machen – mit wenigen Worten darauf antworten können und der Fortgang des Unterrichtsgeschehens so gesichert ist. Als Initiator für aktiv-entdeckendes und konstruktives Lernen scheint diese Art von Unterrichtskommunikation allerdings nicht geeignet (vgl. Krummheuer 2004).
Vor diesem Hintergrund soll im vorliegenden Beitrag die sprachliche Aushandlung in inklusiven Mathematikstunden anhand zweier ausgewählter Unterrichtsszenen betrachtet und analysiert werden. Hierzu wird im Weiteren das gängige methodische Vorgehen der Interaktionsanalyse zur Analyse von Transkripten von Videodaten in der Interpretativen (Unterrichts-)Forschung der Mathematikdidaktik dargestellt. Die verwendeten videographierten und anschließend transkribierten Szenen stammen aus dem Datenmaterial des Habilitationsprojektes von Anke Langner, die von 2011 bis 2013 sieben Grundschulklassen in Nordrhein-Westfalen begleitete (vgl. Langner 2015).
Der vorliegende Beitrag versucht in Anlehnung an neuere Arbeiten der Interpretativen Forschung der Mathematikdidaktik dem Ziel zu genügen eine Veränderbarkeit im nicht zweckrationalisierten und gegebenenfalls habituellen Handeln der Lehrpersonen aufzuzeigen und so Voraussetzungen zu schaffen, die Veränderung von Unterricht nach sich ziehen können. Nur so erscheint es möglich wirkliche Unterrichtsinnovation zu betreiben und ein bis dato weitestgehend unerforschten Bereich des fachdidaktischen Lernens unter inklusiven Bedingungen zu erforschen. Bei all diesen Bemühungen sei erwähnt, dass es sich bei den hier dargestellten Ergebnissen um vorläufige Ergebnisse einer Vorstudie handelt und die Verbindung von fachlicher und sozialer Teilhabe in inklusiven Lehr-Lernsettings des Grundschul-mathematikunterrichts in Deutschland bis dato weitestgehend unerforscht ist.
Auf Basis obiger theoretischer Überlegungen geht die zugrundeliegende Untersuchung folgender forschungsleitenden Frage nach: Welche Möglichkeiten zur fachlichen Teilhabe ergeben sich durch die sprachliche Gestaltung der Lernprozesse durch die Lehrpersonen?
Diese Frage lässt sich anhand zweier spezifizierter Fragen ausdifferenzieren: Was für Sprachanlässe werden den Kindern innerhalb des Unterrichts geboten? und Wie entwickelt sich das mathematische Thema innerhalb dieser sprachlichen ‚Spielräume’?
Als empirische Grundlage des Beitrages dienen Videoaufnahmen von alltäglichem inklusivem Grundschulmathematikunterricht. Zur Analyse der (sprachlichen) Gestaltung des inklusiven Grundschulmathematikunterrichts durch die Lehrperson bzw. für die Analyse der kollektiven Aushandlungsprozesse im Unterricht werden mit Hilfe der Interaktionsanalyse (s. z. B. Krummheuer 2011) Klassengespräche analysiert. Ursprünglich geht die Interaktionsanalyse auf konversationsanalytische Arbeiten aus dem Bereich der Ethnomethodologie zurück (vgl. Eberle 1997; Sacks 1996). Ihren Einzug in den Bereich der Interpretativen Unterrichtsforschung der Mathematikdidaktik hielt die Interaktionsanalyse über Arbeiten von Bauersfeld, Krummheuer und Voigt (1986) und Voigt (1984). Diese ersten Ansätze der Interaktionsanalyse im Bereich der Interpretativen Forschung wurden im Laufe der letzten Jahre für spezielle Fragestellungen durch verschiedene Forscherinnen und Forscher mehrfach modifiziert (vgl. Fetzer 2007, Brandt 2004, Krummheuer & Brandt 2001, Tiedemann 2012). Der sprachlichen Gestaltung des Unterrichts kommt eine besondere Bedeutung zu, da alle Kinder unter Berücksichtigung ihrer individuellen Fähigkeiten in kollektive Argumentationen bestmöglich einzubinden sind. Durch die Interaktionsanalyse kann rekonstruiert werden, wie sich Bedeutungsaushandlungen von Individuen in der Interaktion konstituieren und so zu geteilt geltenden Deutungen werden. Die Interaktionsanalyse dient dazu, Musterhaftes und Strukturen in den verbalen Handlungen der Lehrpersonen und der Kinder zu rekonstruieren und so die Bedingungen der Möglichkeit von fachlichem und sozialem Lernen der beteiligten Kinder zu beschreiben. Durch die Interaktionsanalyse wird es ermöglicht, der Sequentialität dieser Hervorbringung sowie der Reproduktion und Veränderung von Strukturen in den jeweiligen Interaktionsprozessen Rechnung zu tragen.
Angelehnt an die Arbeiten von Bauersfeld, Krummheuer und Voigt (1986) und Voigt (1984) beinhaltet die folgende Interaktionsanalyse folgende Analyseschritte:
Im folgenden Kapitel werden die Analysen und Ergebnisse der Interaktionsanalyse dargestellt.
Äußerer Rahmen der Szene
In dieser Szene ist ein Ausschnitt aus dem Mathematikunterricht in einer ersten Klasse dargestellt. An der videographierten Unterrichtsstunde, die nach der Frühstückspause um 10.15 Uhr beginnt, nehmen 23 Schülerinnen und Schüler – 12 Mädchen und 11 Jungen – teil. Die Hälfte der Kinder sitzt an Gruppentischen, die andere Hälfte an einer zusammenhängenden Tischreihe aus Zweiertischen mit senkrecht angeschobenen Quertischen. Eine zweite Lehrperson ist mit einem Schüler der Klasse im Nebenraum. Eine weitere dritte Lehrperson sitzt in der Mitte des Klassenzimmers zwischen den Schülern und Schülerinnen an einem Zweiertisch mit einer Schülerin. Zu Unterrichtsbeginn verteilt die Lehrperson Wochenpläne an die Schüler und Schülerinnen. Die Kinder kleben ihren individuellen Plan in ein Heft ein und verstauen diesen im Schulranzen. Die Lehrperson fordert die Schüler und Schülerinnen mehrfach zur Ruhe auf und dazu alle Sachen bis auf das Rechenheft wegzupacken. Hiernach beginnt die folgende Unterrichtinteraktion:
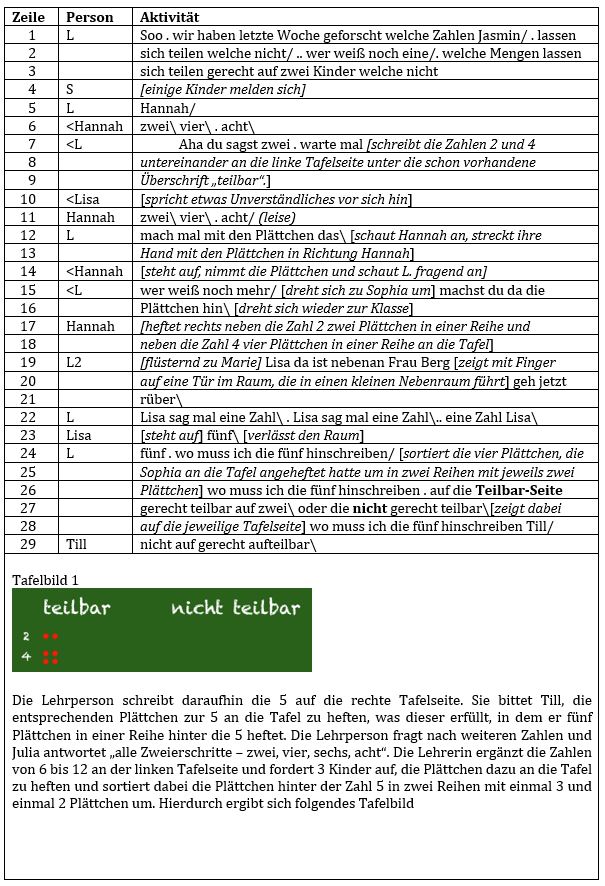

Gliederung der Szene
<1-54> Zahlen, die sich durch Zwei teilen lassen
<55-101> Zahlen, die sich nicht durch Zwei teilen lassen
<102-256> Vergleich der „Teilbar-Seite mit der Nicht-Teilbar-Seite“
<257-281> Ungerade und gerade Zahlen
Zusammenfassung der Interaktionsanalyse <1-29>
Die Lehrperson beginnt den Unterricht mit „Soo . wir haben letzte Woche geforscht welche Zahlen Jasmin/ . lassen sich teilen welche nicht/ .. wer weiß noch eine/. welche Mengen lassen sich teilen gerecht auf zwei Kinder welche nicht“ <1-3>. Hiermit scheint sie einen Bezug zum Unterricht der letzten Woche zu knüpfen und die Kinder zu ermutigen ihre gemachten Entdeckungen zu beschreiben. Der Beginn der Frage ist hierbei etwas unpräzise, da sich zunächst einmal alle Zahlen in der Mathematik teilen lassen. Gehen wir davon aus, das Kinder dieses Jahrgangs bei Zahlen vordergründig an natürliche Zahlen denken, lassen sich diese alle teilen jedoch haben Primzahlen keine echten Teiler, da sie lediglich durch eins und sich selber teilbar sind. Insofern könnte im Weiteren die Behandlung von Primzahlen erfolgen. Am Ende ihrer Äußerung schränkt die Lehrperson die anfängliche Frage allerdings ein „/. welche Mengen lassen sich teilen gerecht auf zwei Kinder welche nicht“. In Bezug auf das Teilen fokussiert die Lehrperson hier auf die Grundvorstellung des Verteilens einer festgelegten Anzahl von Elementen einer Menge M auf eine festangelegte Anzahl an Teilmengen. Mit dem Ausdruck gerecht scheint die Lehrperson zu versuchen das mathematische Konzept der Gleichmächtigkeit der Teilmengen in ein alltagssprachliches Konzept zu überführen. Zielt das Teilen von „Mengen“ eher auf ein abstraktes mathematisches Konzept ab, scheint der Zusatz „gerecht“ eher in die Richtung der Verteilung von Bonbons an Kinder zu weisen. Insgesamt bleibt etwas unklar, ob die Kinder nun einfach beliebige Zahlen nennen könnten oder aber auch noch begründen müssten, warum diese gerecht zu teilen sind. Es melden sich mehrere Kinder von denen Hannah aufgefordert wird. Hannah gibt mit „zwei\ vier\ . acht\“ <6> gleich mehrere Zahlen an. Sie könnte mit ihrer Antwort die Zweierreihe aufzählen und hierbei nur die 6 vergessen oder aber vielleicht mit dem Gedanken der Verdoppelung, die Potenzreihe von zwei aufsagen. Da die Lehrperson Hannah jedoch sofort unterbricht und lediglich die „zwei“ verbal und die zwei und vier durch Anschreiben an der Tafel visuell verstärkt, bleibt Hannahs Begründung für ihre Antwort ungeklärt. Ließ der Beginn des Unterrichts mit dem Verweis auf vorangegangene Forschungsaktivitäten der Kinder einen gewissen mathematischen Anspruch und gegebenenfalls die Reflektion eines offenen Entdeckungsauftrags der letzten Woche erwarten, wird nun der Handlungsspielraum durch die Lehrperson stark eingeschränkt. Ebenso wird der Sprachanlass nun von erwartbaren Begründungen auf das Nennen von Zahlen reduziert. Durch das Anschreiben der Zahlen unter die Überschrift „teilbar“ unternimmt die Lehrperson eine Zuweisung der Zahlen, die sie jedoch nicht begründet <7-9>. Hiernach fordert die Lehrperson Hannah auf, die Zahlen mit Plättchen darzustellen. Dem kommt Sophia nach und klebt hinter die Zahl zwei bzw. vier die jeweilige Anzahl der Klebeplättchen in eine Reihe <12-18>. Ungeklärt bleibt der Grund für dieses Ankleben. Zeitgleich fragt die Lehrperson „wer weiß noch mehr/“ <15> und etwas später „Lisa sag mal eine Zahl\ . Lisa sag mal eine Zahl\.. eine Zahl Lisa\“ <22>. Der mathematische Anspruch scheint sich hierdurch zunehmend zu verringern. Ging es anfangs scheinbar noch um das Berichten von Forschungsergebnissen, werden jetzt von der Lehrperson nur noch weitere Zahlen eingefordert, was in der Handlungsverengung mündet, dass Lisa lediglich irgendeine Zahl zu nennen hat. Um dieser Aufforderung nachzukommen muss Lisa bis zu diesem Zeitpunkt das Unterrichtsgespräch nicht aufmerksam verfolgt haben. Lisa steht auf, sagt „fünf\“ und verlässt anschließend den Raum. Damit gibt sie eine nicht teilbare Zahl in der Kategorisierung der Lehrperson an. Dies könnte dem Ursprung geschuldet sein, dass sie entweder einfach in der Reihenfolge der Natürlichen Zahlen die nächste Zahl folgend auf vier gewählt hat, was bedeuten würde, dass sie aufmerksam gewesen war, gegebenenfalls sogar weiß, dass dies eine Zahl des anderen Bereiches der nicht teilbaren Zahlen darstellt oder aber einfach willkürlich eine Zahl gewählt hat. Während die Lehrperson nun die Plättchen an der Tafel unkommentiert so umsortiert, dass diese in Zweierreihen mit je zwei Plättchen angeordnet sind, fragt sie „fünf . wo muss ich die fünf hinschreiben wo muss ich die fünf hinschreiben . auf die Teilbar-Seite gerecht teilbar auf zwei\ oder die nicht gerecht teilbar“. Hierdurch scheint sich der Anspruch an die Kinder die genannten Zahlen in das Kategoriensystem der Lehrperson an der Tafel örtlich zuzuordnen zu verfestigen. Die Möglichkeit hierbei einen Fehler zu machen oder richtig zu liegen, liegt bei jeweils 50 Prozent. Das zugrundliegende Konzept wird nicht thematisiert, ebenso nicht der Grund der Anordnung der Plättchen und die Kinder sind auch nicht aufgefordert ihre Zuordnung einer Zahl zu einer Tafelseite zu begründen. Zudem fokussiert die Wortwahl der Lehrperson, wo diese die Zahlen hinschreiben muss lediglich auf das Hier und Jetzt der Situation. Eine Allgemeingültigkeit der Zuweisung über die vorliegende Situation hinaus lässt sich aus dieser sprachlichen Form nicht ablesen. In Bezug auf das sprachliche Vorbild, welches die Lehrperson darstellt, fällt insbesondere durch ihre Aussage in <18-19> und <42-43> auf, dass diese eine Fülle von Synonymen für die Beschreibung des Konzeptes der Teilbarkeit durch zwei verwendet und dieses mit alltäglichen Konzept der Gerechtigkeit unerklärt verbindet.
Zusammenfassung der Interaktionsanalyse <55-66>
Während die Lehrperson auf die rechte Tafelseite tippt, fragt sie mit „fallen euch hierzu noch welche ein/ oder ist nur die fünf nicht gerecht teilbar/.. Benjamin/“ nach weiteren nicht teilbaren Zahlen. Da sie die Fünf zuvor unkommentiert an die „Nicht-teilbar-Seite“ geschrieben hat, scheint für sie die Antwort von Till, dass die Fünf zu den nicht gerecht teilbaren Zahlen gehört, unstrittig zu sein. Weiterhin bleibt das mathematische Konstrukt hinter „gerecht“ unthematisiert. So könnte man die Menge 9 auch in drei gleichmächtige Mengen mit je drei Elementen aufteilen. Dies wäre gerecht aber nicht gerecht durch zwei teilbar. Da die Lehrperson in ihrem Tafelbild über der Zahl 5 zwei Stellen freilässt, ist davon auszugehen, dass hier noch zwei nicht teilbare Zahlen zu nennen sind. Nach der Aufforderung von Benjamin gibt dieser mit „sieben\“, die nächst größere nicht durch zwei teilbare Zahl an, welche die Lehrperson sogleich an die Tafel schreibt. Lukas scheint dem jetzigen Verlauf gut gefolgt zu sein und seine Antwort hat eine gute Passung zu dem bis jetzt Ausgehandelten. Hiernach fordert die Lehrperson Timo auf zu sprechen, wobei etwas unklar ist, was Timos Auftrag zu sein scheint. Er könnte nun Benjamin Antwort evaluieren oder aber eine neue Zahl nennen. Timo zeigt auf die linke Tafelseite und sagt „Alle die dazwischen fehlen\.. auch sind nicht durch teil- \ weil jeder Zweite\ erst kommt einer der nicht gerecht teilbar dann einer geteilbar dann einer nicht teilbar dann einer teilbar dann nicht teilbar-“ <60-63>. Ohne das explizit eine verallgemeinernde Begründung für die Zahlen der „Nicht-durch-zwei-teilbar-Seite“ von der Lehrperson erfragt wird, evaluiert Timo nicht nur die Äußerung von Benjamin, sondern hebt diese auf eine allgemeingültige Ebene. Er erkennt den Zusammenhang zwischen den Zahlen und gibt an, dass jede zweite Zahl immer auf einer Seite stehen würde. Insofern erscheint seine Antwort äußerst bemerkenswert. Auffällig scheint seine Wortwahl bzw. seine Schwierigkeiten seine Entdeckung in eine passende Wortwahl zu überführen. Dies lässt sich eventuell auf die vielen synonymen Begrifflichkeiten zurückführen, die die Lehrperson seit Beginn des Unterrichts verwendet. So verwendete die Lehrperson bis jetzt: teilen, aufteilen, teilbar und nicht teilbar (steht an der Tafel), gerecht teilbar, gerecht auf zwei Kinder, gerecht teilbar durch. Aber auch der mathematisch hohe Anspruch der Aussage von Timo, könnte ein Grund sein, dass dieser seine Aussage nicht einfach in Worte zu fassen vermag. Timo macht daraus: durch teil-, nicht gerecht teilbar, geteilbar, nicht teilbar und teilbar, was seine Bemühungen verdeutlicht, die Entdeckungen exakt zu erklären aber auch seine Schwierigkeiten die richtige Formulierung hierfür zu finden. Obwohl Timo nicht nur eine Zahl genannt hat und eher auf einer ersten Stufe der Verallgemeinerung Zusammenhänge beschrieben hat, wird diese Leistung von der Lehrperson nicht positiv evaluiert. Im Gegenteil, sie schreibt nun drei weitere Zahlen, 1, 3 und 9, an die Tafel und fragt „Wie geht’s weiter/. ich hab schon ein bisschen verraten jetzt grad ganz viel . wie geht’s weiter/“. Sie greift damit weder die Erklärungsversuche noch seine Schwierigkeiten bei der Formulierung auf. Hierdurch scheinen die Kinder in dieser Szene immer mehr in die Rolle von Statist_innen gedrängt zu werden und die Lehrperson führt Regie, in dem von ihr vorher geplanten Unterrichtsskript. Es wird eine Art von offenem Unterricht inszeniert, der den Charakteristika eines solchen jedoch nicht entspricht, denn weder Entdeckungen noch die Begründung für die entdeckten Muster und Strukturen finden einen Raum in diesem. Timo hat mit seiner Begründung nahezu alle entscheidenden Zusammenhänge erklärt. Mithilfe seiner Begründung kann ausgehend von einer Startzahl jede weitere Zahl eindeutig als ungerade oder gerade bestimmt werden. Sie verdeutlicht außerdem, dass nie zwei gerade oder ungerade Zahlen aufeinander folgen können.
Zusammenfassung der Interaktionsanalyse <102-129>
Kurz vor diesen Zeilen nennen einige Kinder weitere Zahlen, welche diese und andere Kinder anschließend mit Hilfe von Plättchen an der Tafel darstellen <67-101>. Diese Handlungen werden von der Lehrperson erneut unkommentiert berichtigt, so dass alle Zahlen in Zweierreihen dargestellt werden. Im Anschluss hieran sagt die Lehrperson „Und dann könnt ihr euch das mal angucken an der Tafel\ was fällt dir auf/“ <102-103>. Diese Aussage bzw. Frage der Lehrperson verwundert insofern, da Timo sie bereits ohne Aufforderung zuvor beantwortet hatte. Somit könnte dies eine Form des erneuten Aufgreifens seiner Entdeckungen und Begründungen sein. Ein nicht zu identifizierendes Kind antwortet „Ähhm- bei bei den ist immer- bei den Ungeraden ist immer . ist immer\ also sag ich mal da ist da äh das ist vier bei der drei ist“ <104-107> und zeichnet anschließend mit dem Finger etwas in die Luft. Diese Aussage lässt sich nicht zweifelsfrei deuten. Eine Deutung wäre, dass das Kind versucht eine Eins-zu-Eins-Zuordnung der unterschiedlichen Zahlen vorzunehmen. Eindeutig scheint, dass es die Zahlen miteinander in Bezug setzt und ebenfalls Muster erkennt. Auffällig scheint zudem die Wortwahl „Ungeraden“. Dieser Begriff ist zum jetzigen Zeitpunkt nicht gefallen und stellt ähnlich, wie die Äußerung von Timo eine äußerst innovative Leistung des Kindes dar, denn das Kind überträgt, die eher alltagssprachlich gewählten Bezeichnungen der Lehrperson mit Handlungsbezug auf den korrekten mathematischen Fachterminus. Die Lehrerin reagiert auf diese nicht einfach zu verstehende Äußerung des Kindes und bittet dieses nach vorne zu kommen und es zu erklären <107>. Das Kind kommt nach vorne, zeigt an der linken Tafelseite auf die vier Plättchen und danach auf die drei an der rechten Tafelseite und sagt „bei der vier sind\ bei der vier und bei der drei ist nur eine weniger\“ <108-110>. Mit dieser Aussage, sagt das Kind etwas, was bereits geteilt geltendes Wissen der Kinder zu sein scheint, nämlich, dass die drei einer weniger als die vier ist und bezieht sich damit eventuell auch auf die figurierte Darstellung dieser Zahlen. Weiter lässt sich nicht rekonstruieren, was das Kind auszusagen versucht. Es könnte sein dass es sprachliche Schwierigkeiten hat seine Entdeckungen in Worte zu fassen oder aber, dass für das Kind die Frage beantwortet scheint und es aus seiner Perspektive aufgrund der offenen Fragestellung der Lehrperson keinen Bezug zur Teilbarkeit angeben müsse. Die Lehrperson geht auf diese Äußerung erneut nicht ein und negiert sowohl die sprachlichen Probleme als auch die Möglichkeit die Entdeckungen dieses Kindes für alle nutzbar zu machen. Es scheint als werde Teilhabe aller inszeniert, ohne, dass die inhaltlichen Beiträge dieser Teilhabe der Kinder in den Unterrichtsdiskurs von der Lehrperson integriert werden. Hierdurch emergiert keine kollektive Argumentation, sondern eine Vielzahl unverbundener Aussagen der Kinder, die bis zum jetzigen Zeitpunkt von ihnen selber inhaltlich verbunden werden müssen. Das Skript der Lehrperson scheint einen roten Faden zu haben, was sich unter anderem anhand ihrer stetigen Bemühungen zeigt, die Plättchen in bestimmter Reihenfolge anzuordnen. Dieser rote Faden kann und wird jedoch nicht von den Kindern aufgegriffen bzw. versucht die Lehrperson nicht diesen mit den Deutungen der Kinder zu koordinieren. So fährt sie mit dem Unterrichtsgespräch wie folgt weiter, während sie auf die linke Tafelseite zeigt „wir wollten gerade besprechen was uns auffällt wenn wir die linke Seite wenn wir die Plättchen der linken Seite mit den Plättchen der rechten Seite vergleichen\ ... Merle und Celina passt doch jetzt mal bitte auf wenn ihr was zum Thema sagen wollt dann sagt es laut\ .. Till\“. Mit dieser Aussage greift die Lehrperson nun die vielfachen Bemühungen auf, eine Beziehung zwischen den Zahlen der beiden Tafelseiten herzustellen – dies aber ohne Bezug zur Teilbarkeit der Zahlen. Sie geht jedoch nicht auf eine der diesbezüglichen Äußerungen der Kinder ein. Till sagt „Da kann alles in eine Lücke rutschen\ .. Also“. Diese Aussage könnte sich darauf beziehen, dass die Zahlen auf der „Nicht-teilbar-Seite“ keine abschließende Darstellung durch eine Zweierreihe haben und ein Plättchen fehlt. Möglich wäre auch, dass Till darauf hinweist, dass man zwei ungerade Zahlen durch zusammenschieben der beiden Plättchendarstellungen in die jeweiligen Lücken zu einer Plättchendarstellung zusammenführen kann, die keine Lücke enthält. Die Lehrperson fordert Till auf, nach vorne zu gehen und seine Aussage zu erklären <122-123>. Er tut dies und beginnt bereits beim Laufen zu sagen „das können wir dahin rutschen\“ <124-125>. Seine Aussage lässt nun keine weitere Deutung als zuvor zu. Die Lehrperson greift diese vermeintlich auf und sagt „Du meinst dass ist immer so im Wechsel\ eins- zwei- drei-.. meinst du das/“ während sie abwechselnd auf die Tafelseiten zeigt. Erneut scheint sie nicht auf die zuvor getätigte Aussage eines Kindes einzugehen, denn sie paraphrasiert hier nicht die Aussage von Till, sondern die von Timo <60-63> und ‚legt’ diese Till sprichwörtlich in den Mund, da sie eventuell eine momentan günstige Passung zu ihrem Unterrichtsskript aufweist. Till bleibt auf diese einengende Suggestivfrage kaum ein anderer Spielraum als sie zu bestätigen, wonach die Lehrperson wieder alle Kinder nach weiteren Auffälligkeiten fragt <128-129>.
Zusammenfassung der Interaktionsanalyse <257-281>
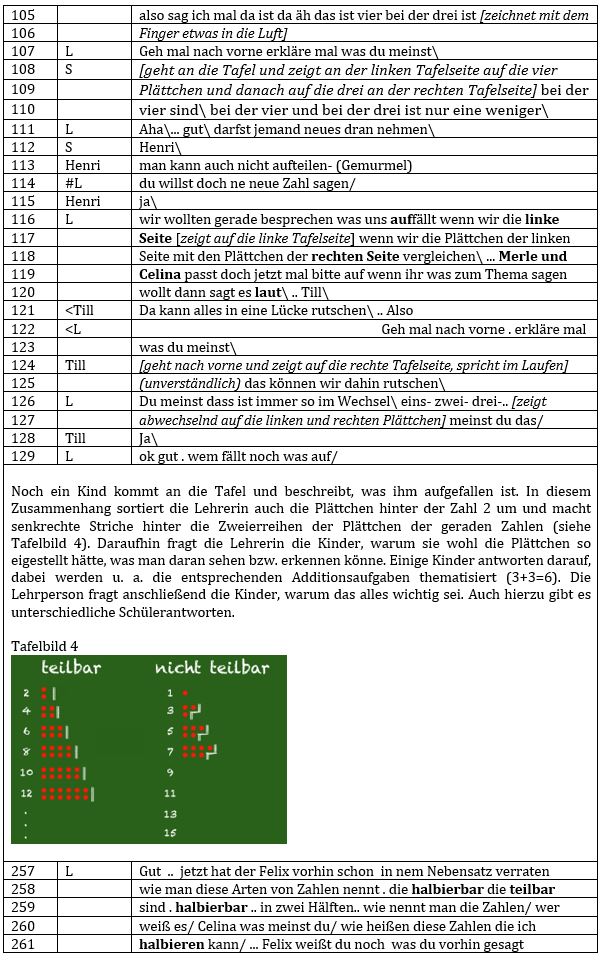
Kurz vor den nun folgenden Handlungen fragt die Lehrperson die Kinder, warum sie wohl die Plättchen so eigestellt hätte und was man daran sehen bzw. erkennen könne. Einige Kinder antworten darauf, dabei werden u. a. die entsprechenden Additionsaufgaben thematisiert (3+3=6). In diesem Zusammenhang sortiert die Lehrperson auch erneut die Plättchen und macht senkrechte Striche hinter die Zweierreihen der geraden Zahlen und eine Art Treppenstufe hinter die Plättchendarstellung der ungeraden Zahlen (siehe Tafelbild). Die Lehrperson fragt anschließend die Kinder, warum das alles wichtig sei. Auch hierzu gibt es unterschiedliche Schülerantworten <130-256>. Daraufhin beginnt die folgende Sequenz der Aussage der Lehrperson „Gut .. jetzt hat der Felix vorhin schon in nem Nebensatz verraten wie man diese Arten von Zahlen nennt . die halbierbar die teilbar sind . halbierbar .. in zwei Hälften.. wie nennt man die Zahlen/ wer weiß es/ Celina was meinst du/ wie heißen diese Zahlen die ich halbieren kann/ ... Felix weißt du noch was du vorhin gesagt hast/“ <257-262> und fordert nach kurzer Pause Luke auf zu sprechen. Obwohl ein Kind zuvor bereits den Fachterminus „die Ungeraden“ benutzte, der von der Lehrperson nicht aufgegriffen wurde, fragt sie nun nach dem korrekten Fachterminus für die gerecht durch zwei teilbaren Zahlen. Luke kommt dieser Aufforderung nach und sagt etwa zögerlich, dass dies die geraden Zahlen seien <263>. Die Lehrerin geht erneut nicht auf die Antwort des Schülers ein und sagt „wo sieht man das sofort dass das gerade Zahlen sind/ wer kann mal nach vorne kommen und das zeigen … Fiete komm . wo sind die geraden Zahlen/…und dann können wir alle überlegen wie die hier wohl heißen“ <264-267>, zeigt auf die rechte Seite der Tafel. Auffällig scheint hier vor allem der anfängliche Bezug zwischen ihrer Visualisierung und dem Verständnis der Kinder. Sie suggeriert demnach, man könne aus einer Visualisierung sofort erkennen, wofür diese ist bzw. welches Konzept diese transportiert. Im Weiteren wird dieser Anspruch durch die Lehrperson jedoch dahingehend reduziert, dass es erneut nur darum geht „wo die gerade Zahlen sind“ und weiter wie diese „heißen“. Hier scheint sich ein weiteres alltagspädagogisches Verständnis der Lehrperson zu offenbaren. Die Bezeichnungen von Fachbegriffen ebenso wie mathematische Konventionen lassen sich im Gegensatz zu mathematischen Mustern oder Strukturen eben nicht entdecken. Das bedeutet, dass an Stellen, wo es etwas zu entdecken gab und die Kinder, wie z.B. Timo ihre Entdeckungen sogar versucht haben zu verbalisieren, die Lehrperson dies nicht aufgegriffen hat und nun einen entdeckenden Zugang zu initiieren scheint an einer Stelle, wo es nichts zu entdecken gibt. Abschließend fragt die Lehrperson wie die anderen Zahlen „heißen“, was jedoch bereits zuvor von einem Kind ungefragt beantwortet wurde. Auf die Antwort von Julian <271> „schräge Zahlen\“ bessert Celina mit „ungerade Zahlen\“ <273> nach. Julian macht gegebenenfalls ein Sprachspiel auf und versucht das sprachliche Pendent zu gerade zu finden. Diese Herleitung des Fachterminus hat eine gewisse Logik, führt jedoch nicht zum erwünschten Fachbegriff. Celina scheint die korrekte Bezeichnung zu kennen oder diese zuvor von einem Kind gehört zu haben und verbessert Julian. Fiete ergänzt „das ist so weil hier der Strich gerade ist kann man das erkennen und da eckig nicht gerade\“. Hier nimmt Fiete anscheinend Bezug auf die Visualisierung der Lehrperson, welche senkrechte Striche hinter die Plättchendarstellung der geraden Zahlen und Treppenstufen hinter die ungeraden Zahlen machte. Er scheint die Visualisierung mit dem Fachterminus der Zahlen in Verbindung zu setzen und die Fachtermini für die beiden Zahlenarten aus ihrer Visualisierung abzuleiten. Fiete bestärkt anscheinend Celinas Aussage, indem er eine explizite Begründung angibt. Das Pendant zu gerade bezeichnet er jedoch mit eckig. Neben dem Problem, dass die Fachtermini aus der Visualisierung nicht herzuleiten sind, ergibt sich des Weiteren noch die Problematik, dass die Kinder im Hier und Jetzt des Unterrichts bleiben und das Konzept nicht generalisierbar erscheint, denn nur Zahlen, deren Plättchendarstellung mit einem geraden Strich kennzeichenbar sind, scheinen gerade Zahlen zu sein – dass dies auch von der gewählten Darstellungsweise abhängig ist und man bspw. neben die Eins auch einen geraden Strich machen könnte, bleibt unthematisiert. Eine abzuleitende verallgemeinerbare Regel über die Situation lässt sich so nicht herleiten.
Die Lehrperson entgegnet auf diese sich zum ersten Mal entwickelnde kollektive Argumentation von einigen Kindern mit „Mhh genau super . da sind die geraden Zahlen die lassen sich ganz gerecht in zwei Hälften teilen . halbieren und da sind die ungeraden Zahlen . da gibt’s immer so ne Ecke drin-.. die müsste man entweder durchschneiden-. Oder wegpacken-. oder was dazutun- damit man es vernünftig halbieren kann\ du suchst bitte den buntes Rechenbuch raus\“ <276-281> während sie auf die linke Tafelseite zeigt. Etwas überraschend greift die Lehrperson hier die Begründung von Fiete auf und lobt anscheinend diese und Celina. Sie wiederholt, dass die gerade Zahlen sich in zwei Zahlen teilen lassen, was sich als Ergebnissicherung deuten lässt. Als Begründung hierfür scheint jedoch nun der gerade Strich zu fungieren, welcher das mathematische Konzept des Teilens in gleichmächtige Mengen nicht zu visualisieren vermag. Hiernach greift die Lehrperson explizit die Begründung mit der „Ecke“ von Fiete auf. Diese erscheint für das mathematische Konzept von ungeraden Zahlen nicht tragfähig – eben so wenig wie das Bild, dass man bei ungeraden Zahlen etwas „durchschneiden“ oder „wegpacken“ müsse. Letztere Ausdrücke suggerieren, dass es sich bei ungeraden Zahlen um unfertige, fehlerhafte und zu reparierende Zahlen handeln würde. Hierbei ergeben sich zwei Problematiken. Neben der Tatsache, dass die Visualisierung lediglich versucht die Benennung des Fachbegriffs zu erklären und diese nicht tragfähig erscheint, erhebt diese keinen Anspruch auf Allgemeingültigkeit. So ist nicht zu erkennen, wie die Zahl Eins mit dieser Logik zuzuordnen wäre und Zahlen, die nicht an der Tafel visualisiert sind, werden damit ebenfalls schwer zuordbar. Ob sie nun einen geraden Strich oder eine Ecke hätten, müsste man wieder erneut über Visualisierungen herausfinden. Mithilfe des entdeckten Musters von Timo, welches nicht weiter thematisiert wurde, ließen sich hingegen alle weiteren Zahlen auf induktiver Weise zuweisen.
Theoriereflexion
In der Szene scheint die Lehrperson, auf einem neuen Bild von Mathematik fußend, die Reflektion einer zuvor durchgeführten aktiv entdeckenden Unterrichtseinheit zu initiieren, indem sie nach den Forschungsergebnissen der Kinder fragt. Innerhalb der Interaktion mit den Kindern entspinnt sich jedoch etwas anderes. In der ersten Unterrichtsphase müssen die Kinder nur Zahlen nennen und diese einer Tafelseite zuweisen. Begründungen und Entdeckungen, die von ihnen teilweise sogar ohne Aufforderung eingebracht werden, werden nicht von der Lehrperson aufgegriffen oder hinterfragt. Insofern bleiben die zum Teil fachlich anspruchsvollen Entdeckungen der Kinder inhaltlich unverbunden. Die Aushandlung der mathematischen Begriffe bleibt im Hier und Jetzt und es lassen sich keine Versuche der Lehrperson ausmachen, die Konzepte vom Situativen auf eine allgemeingültigere Ebene zu übertragen, obwohl dies z.B. in Timos Aussage angelegt ist. Insofern wird trotz der Behandlung eines mathematischen Konzeptes, was sich gängiger Weise durch einen hohen Grad an Generalisierung, einer Loslösung von der Situation, auszeichnet, dieser für Kinder wichtige zu lernende mathematische Aspekt nicht berücksichtigt (vgl. Gellert 2011, Jung & Schütte 2016, 2015).
Es entwickelt sich ein Interaktionsmuster, welches dem Trichtermuster (Bauersfeld 1978) ähnelt, und es lässt sich teilweise das Musters der inszenierten Alltäglichkeit (Voigt 1984) rekonstruieren. Charakteristika dieser Zuordnung sind die starken Handlungsverengungen, die durch die Lehrperson durchgeführt werden, in denen gerade keine Entdeckungen oder eigenen Zugänge der Kinder gefragt sind, sondern kurztaktige kleinschrittige Antworten auf die von der Lehrperson gestellten scheinbar offenen Fragen. Der Inszenierungscharakter wurde bereits in der ausführlichen Analyse herausgearbeitet. Die Lehrperson inszeniert hier eine offene Form der Aushandlung in der es jedoch nur darum geht Zahlen zuzuweisen und nicht darum mathematische Konzepte zu verstehen. Betrachtet man die interaktiven Wechselbeziehungen der Beteiligten, lassen sich - mit Verweis zum theoretischen Rahmen dieses Artikels – keine kollektiven Argumentationen (Krummheuer 1992, Miller 1986) der Kinder rekonstruieren. Die Aussagen der Kinder scheinen meist keinen Bezug aufeinander zu haben und werden auch nicht von der Lehrperson koordiniert, so dass sich eine kollektive Argumentation entfalten könnte.
In Bezug auf die sprachliche Gestaltung dieser Unterrichtssituation fällt auf, dass die Lehrperson durch ihre scheinbar offenen Fragen und das intensive Einbinden der Kinder viele Sprachanlässe schafft. Sie greift die sprachlichen Versuche der Kinder ihre Entdeckungen zu beschreiben jedoch fast nie auf, was besonders auffällig bei den Versuchen von Timo hervortritt. Hierdurch werden die Bemühungen der Kinder nicht wertgeschätzt und münden schlussendlich auch kaum in einem sprachlichen Lernzuwachs. Des Weiteren stellt die Lehrperson kein sprachliches Vorbild für die Kinder dar (vgl. Schütte 2009). So verwendet sie bei ihren Fragen und den Erklärungsversuchen eine Vielzahl von synonymen Fachtermini oder Abwandlungen von diesen, die ein Verständnis der Begriffe erschweren. Hiermit vermittelt die Unterrichtssituation ein Bild von Mathematiklernen, welches in einem neuen Gewand auftritt jedoch in weiten Stellen klassische Zugänge vermittelt, indem die gleich zu Beginn aufkommenden fachlich interessante Äußerungen der Schülerinnen und Schüler zugunsten eines kleinschrittigen Vorgehen von der Lehrperson auf das Aufsagen von Zahlen begrenzt werden. Insofern erscheinen die Frage und Impulstechniken der Lehrperson (vgl. Krauthausen & Scherer 2007) keine interaktionalen Verdichtungen initiieren zu können bzw. Möglichkeiten zu diesen. Die Begründungsversuche einiger Kinder werden zu Gunsten des reibungslosen Ablaufs des Unterrichts nicht zum Gegenstand der Aushandlung (vgl. Krummheuer 2002).
Äußerer Rahmen der Szene „Größer-Kleiner“
In dieser Szene ist ein Ausschnitt aus dem Mathematikunterricht in einer zweiten Klasse dargestellt. An der videographierten Unterrichtsstunde nehmen 22 Schülerinnen und Schüler – 11 Mädchen und 11 Jungen – teil. Es ist die erste Unterrichtsstunde der Kinder für diesen Tag. Zu Beginn der Unterrichtsstunde ruft die Lehrperson alle Kinder in einem Sitzkreis vor der Tafel zusammen. Dort findet die Begrüßung statt und die Kinder bekommen in den ersten zehn Minuten die Gelegenheit sich gegenseitig von dem am Vortag stattgefundenem Martinsumzug zu berichten. Anschließend gehen die Schüler und Schülerinnen nach und nach ruhig wieder zurück auf ihre Plätze an die Gruppentische und die Lehrperson beginnt den Mathematikunterricht mit den Worten „So dann schaut bitte mal alle an die Tafel“. Es entspinnt sich folgende Interaktion:

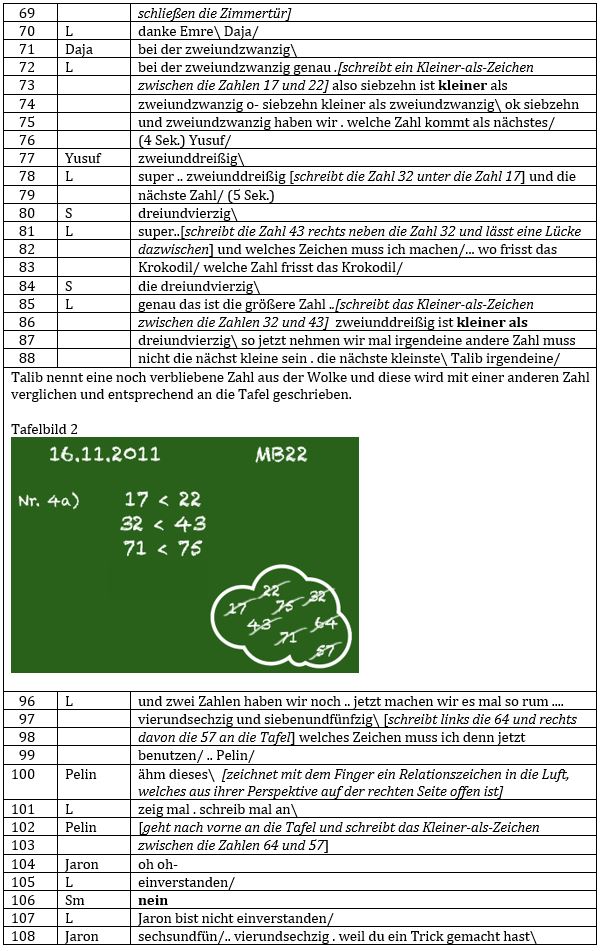

Gliederung
<1-54> Zweistellige Zahlen
<55-97> Kleiner-als-Relation
<98-125> Größer-als-Relation
Zusammenfassung der Interaktionsanalyse <1-16>
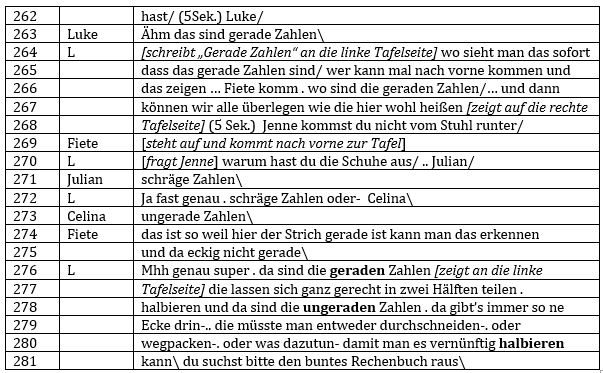
Die Lehrperson beginnt den Mathematikunterricht mit „so dann schaut ihr bitte alle mal an die Tafel\ wer kann denn eine Zahl aus der Wolke einmal vorlesen/“ und ruft einen sich daraufhin meldenden Schüler auf <1-2>.Hiermit gibt sie den Kindern gleich zu Beginn die Möglichkeit sich aktiv am Unterricht zu beteiligen. Der Rahmen dafür ist klar definiert, es geht um das Nennen einer Zahl. Die Anforderungen an die sprachliche Äußerung scheinen dabei sowohl aus fachlicher als auch aus sprachlicher Perspektive für Schülerinnen und Schüler einer zweiten Klasse nicht groß zu sein. Offen bleibt an dieser Stelle zunächst, warum die Zahlen in einer Wolke an der Tafel angeschrieben sind und ob dies nur eine Übung der Zahlwörter darstellt, oder nach dem Nennen einer Zahl, damit noch etwas anderes gemacht wird.
Nachdem Emre zunächst an die Hausaufgabenkontrolle erinnert, nennt er eine Zahl und scheint unsicher zu sein, ob seine Äußerung damit schon der Aufforderung der Lehrperson genügt „äähm . siebzehn uuund-“ <6>. Hiernach weist die Lehrperson noch einmal darauf hin, dass sie nur eine Zahl hören möchte und schnell ein nächstes Kind aufgerufen werden soll „eine Zahl\ ne/ gib weiter ganz schnell\“<7>. Damit sorgt sie dafür, dass möglichst viele Kinder die Chance haben sich sprachlich zu beteiligen und verweist auf die engen Grenzen des sprachlichen Spielraums der Kinder. Es könnte in der Aufforderung „schnell weiter zu machen“ auch zum Ausdruck kommen, dass auch die Lehrperson den geringen fachlichen Anspruch der Aufgabe beachtet und sie nicht viel Zeit mit einer so leichten Aufgabe verbringen möchte. Im Folgenden werden noch drei weitere Kinder aufgerufen, die jeweils eine Zahl aus der Wolke vorlesen. Die Lehrerin bestätigt die Schüleräußerungen jedes Mal kurz und erinnert dabei auch immer daran ein nächstes Kind (schnell) aufzurufen <8-16>.
Zusammenfassung der Interaktionsanalyse <55-88>
In Zeile 55 führt die Lehrperson das Unterrichtsgespräch wieder auf die mathematische Aufgabe zurück, nachdem zuvor ein kurzer Exkurs über das Anschreiben des Datums an der Tafel stattgefunden hat. Sie wiederholt die Aussage von Birkan „Birkan hat gesagt die kleinste Zahl ist die siebzehn . die schreib ich schon mal auf\“ und stellt eine neue Frage „welches ist die Zahl die am nächsten an der siebzehn dran ist/“ <55-57>. Das sprachliche Muster, dass die Schülerinnen und Schüler eine Zahl nennen sollen, verändert sich demnach in dieser Unterrichtsequenz nicht. Der fachliche Anspruch steigt allerdings, da nun nicht mehr nur irgendeine Zahl aus der Wolke vorgelesen werden soll, sondern die zu nennende Zahl bestimmten Eigenschaften, in diesem Fall einer bestimmten Größer-Kleiner-Relation, genügen muss. Pelin scheint auf die Frage mit einer Zahl zu antworten, die nicht in der Wolke zu finden ist. Daraufhin schränkt die Lehrperson ihre ursprüngliche Frage ein, indem sie angibt, dass nur die Zahlen aus der Wolke als zulässige Antworten in Frage kommen „nee hier von den Zahlen meine ich\“ <60>. Pelin korrigiert darauf hin sofort ihre Antwort mit „zweiundzwanzig“ <61>. Die schnelle Reaktion lässt vermuten, dass ihre vorige Antwort nicht den Ursprung in einem fehlenden fachlichen Verständnisses hatte, sondern ihr nur der Rahmen der Aufgabenstellung unklar war. Nachdem nun die beiden Zahlen 17 und 22 an der Tafel stehen, fragt die Lehrperson erneut, welche der beiden Zahlen größer sei „welche Zahl ist den jetzt größer Enis/ welche Zahl ist gröößer Easton/“ <63>. Hier und schon in den Zeilen zuvor <55,57> fällt auf, dass die Lehrperson sprachlich durch eine verstärkte Betonung den Begriffen „größer“, „kleinste“, „am nächsten“ besondere Bedeutung verleiht.
Mit der Frage „wo muss ich also wenn ich das Grööößerzeichen hinmachen/“ in Zeile 66 entsteht kurzzeitig der Eindruck nun würde eine neue sprachliche Anforderung an die Schüler und Schülerinnen gestellt. Spätestens bei der Konkretisierung dieser Frage auf „wo macht das Krokodil das Maul auf/“ wird allerdings klar, dass auch hier die Schüler und Schülerinnen nur die entsprechende Zahl zu nennen haben, so dass die Antwort von Daja wiederrum nicht viel mehr als eine Nennung der Zahl ist „bei der zweiundzwanzig“ <71>. Dieses Fragemuster behält die Lehrperson bis Zeile 96 bei und es kommen drei weitere Kinder zu Wort, die jeweils eine Zahl nennen <77, 80, 84>. Die Lehrperson behält ebenfalls bei, dass sie abschließend die jeweiligen Zahlbeziehungen sprachlich noch einmal hervorhebt und dabei die entsprechenden Schlüsselwörter betont, z.B. „zweiunddreißig ist kleiner als dreiundvierzig\“ <86>. Sie scheint sich an dieser Stelle ihrer Rolle als sprachliches Vorbild für die Kinder bewusst zu sein, sie initiiert allerdings keine Sprachanlässe in denen die Kinder diese sprachliche Muster üben und von ihr übernehmen können. Die Schülerinnen und Schüler sind so produktiv mathematisch und sprachlich auf eher niedrigem Niveau aktiv tätig. Anspruchsvollere Anforderungen an sie werden vor allem in Form von Rezeptionen sprachlich umfassender Sätze der Lehrperson an sie gestellt. Aus mathematischer Perspektive sei zudem angemerkt, dass die Verwendung der Begrifflichkeit „Größerzeichen“ in Zeile 66 an dieser Stelle fachlich problematisch ist. Durch den Begriff „Größerzeichen“ bzw. „Größer-als-Zeichen“ ist die Richtung des Relationszeichen „>“ fest definiert. Die Frage, wo das Größerzeichen hin muss, könnte somit nur korrekt mit „zwischen die beiden Zahlen“ beantwortet werden – hinzu kommt, dass zwischen die Zahlen 17 und 22 ein Kleiner-als-Zeichen eingesetzt werden müsste 17 < 22 und die Lehrperson im Folgenden an der Tafel schriftlich auch Kleiner-als-Zeichen anschreibt. Durch das Ausweichen auf die alltagssprachlich formulierte Frage, wo das Krokodil sein Maul aufmachen muss, wird dann suggeriert, dass Größer-als-Zeichen sei variabel einsetzbar - einmal nach rechts und einmal nach links geöffnet. Unabhängig davon lässt sich über den didaktischen Mehrwert dieses Bildes des Krokodils für das Relationszeichen streiten, da es den Aufbau des fachlichen Konzeptes der Zahlrelationen und den zugrunde liegenden Ungleichungen nicht explizit unterstützt (siehe alternative didaktische Aufbereitung bei Lauter 1995). Eventuell stellt es aber eine kindliche Merk- und Kommunikationshilfe für die Verwendung mathematischer Symbolsprache dar.
Zusammenfassung der Interaktionsanalyse <98-125>
Durch die Frage „welches Zeichen muss ich denn jetzt benutzen/“ <98,99> werden zum ersten Mal sowohl auf der fachlichen als auch auf der sprachlichen Ebene, die zuvor etablierten Muster durchbrochen. Die Antwort auf diese Frage kann nun sprachlich nicht mehr nur durch die Nennung einer einzelnen Zahl erfolgen. Fachlich steigt der Anspruch insofern, dass die Lehrperson die Reihenfolge der angeschriebenen Zahlen ändert. Auf diesen Wechsel weist die Lehrperson hin „jetzt machen wir es mal so rum“ <96>. Hierbei klärt sie jedoch nicht, was „es“ ist, wodurch nur den Kindern, die der kollektiven Aushandlung des Unterrichts inhaltlich gefolgt sind, dieser Wechsel auffallen müsste. Wurde bisher an der Tafel nur das Kleiner-als-Zeichen verwendet, muss nun zwischen den beiden Zahlen 64 und 57 ein Größer-als-Zeichen eingefügt werden. Pelin scheint mit der neuen Anforderung überfordert zu sein, was sich in ihrer Äußerung „ähm dieses\“ <100> zeigt. Sie weicht an dieser Stelle auf nonverbale Kommunikationsmittel, eine Zeigegestik, aus. Eine mathematisch korrekte Antwort auf die Frage, wäre „Man muss das Größer-als-Zeichen verwenden.“ gewesen. Da die Lehrperson die Begrifflichkeit Größer-als-Zeichen allerdings selbst zuvor nur einmal in Zeile 66 verwendet hat und dabei mathematisch nicht mal ganz korrekt, haben die Kinder für eine solche Antwort kein explizites sprachliches Vorbild. Die Antwort von Pelin kann auf diesem nonverbalen Level allerdings nichtevaluiert werden und die Lehrperson bittet sie, ihre Lösung an der Tafel anzuschreiben „zeig mal . schreib mal an\“ <101>. Die Lehrperson gibt an dieser Stelle keine sprachlichen Hilfestellungen sondern verweist ebenfalls auf „das Zeigen“.
Nachdem Pelin ein Kleiner-als-Zeichen zwischen die Zahlen 64 und 57 geschrieben hat, bekundet Jaron durch die Äußerung „oh oh“ <104> und auf Nachfrage der Lehrperson „Jaron bist nicht einverstanden/“ <107>, dass er mit der Lösung von Pelin nicht einverstanden ist. Dabei fällt auf, dass er zwar das mathematische Konzept verstanden zu haben scheint, es ihm aber nicht gelingt, sein Nichteinverstandensein mit der Lösung von Pelin angemessen zu verbalisieren „sechsundfün/.. vierundsechzig . weil du ein Trick gemacht hast\“ <108>. Er scheint nicht in der Lage die Relationsbeziehung zwischen den beiden Zahlen sprachlich zu beschreiben. Die Lehrerin greift auch an dieser Stelle die sprachlichen Schwierigkeiten nicht auf, sondern bitte Pelin das angeschriebene Relationszeichen mit einem Schwamm von der Tafel zu entfernen „nimm mal den Schwamm\“ <109>. Sie gibt Pelin die Chance ihren Fehler selbst zu berichtigen „Pelin überleg noch mal wie muss das Zeichen jetzt sein/“ <112,113>. Die Verwendung des Wortes jetzt in der Formulierung suggeriert einerseits, dass hier etwas situatives ausgehandelt wird, was nicht unbedingt in einer anderen Situation noch Bestand haben muss und andererseits kann es als Hinweis gesehen werden, dass die Antwort eigentlich schon klar ist, da ja eins der beiden auszuwählenden Relationszeichen nicht mehr in Frage kommt. Es wird jedoch nicht inhaltlich geklärt, warum das Kleiner-als-Zeichen „jetzt“ falsch war. Erst im Nachhinein fragt die Lehrperson Pelin nach einer Begründung, welche darauf hin mit „weil die…vierundsiebzig größer ist\“<117> antwortet und dies auf die Nachfrage „die vierund/“ mit „ähh . sechzig“- korrigiert. Es bleibt unklar, ob Pelins Schwierigkeiten bei der Verwendung des Relationszeichens – auf symbolischer Ebene - oder bei der Bestimmung der Zahlenreihenfolgen – auf mathematischer Ebene- zu verorten sind. Dass sie in Zeile 61 die nächst größere Zahl von 17 ohne Schwierigkeiten bestimmen konnte, und nach dem Fehler angeben kann, dass 64 die größere Zahl ist, deutet darauf hin, dass ihre Schwierigkeiten eher auf der Ebene der Verwendung der symbolischen Fachsprache liegen.
Anscheinend ausgelöst durch das veränderte Interaktionsmuster und die explizite Klärung der aufgekommenen Schwierigkeiten, meldet sich Behram zu Wort „ich will noch was sagen\“<121>. Mit seiner Äußerung „und weil da ist fünfzig und da ist sechzig . kann man wissen\“ <123> scheint er an die Begründung von Pelin anzuschließen und die Frage nach dem Warum zu beantworten. Auch er, der das mathematische Konzept der Zahlrelationen verstanden zu haben scheint, verwendet allerdings sprachlich keine Relationsformulierung. Mit der Formulierung „da ist fünfzig und da ist sechzig“ anstatt der Formulierung fünfzig ist kleiner als sechzig verweist er sprachlich nur auf zwei vorhanden Zahlen, ohne eine Beziehung zwischen ihnen zu beschreiben. Die Lehrperson lobt Behram, wiederholt seine Äußerung und fügt die Erklärung „und da weißt du die ist kleiner ne/“ <125> hinzu. Zum Abschluss weist die Lehrperson noch einmal ausdrücklich auf die Formulierung der Relationsbeziehungen hin, indem sie die Symbolsprache der an der Tafel stehenden Ungleichungen verbalisiert „genau also hier. steht einundsiebzig ist kleiner als fünfundsiebzig .. vierundsechzig ist größer als siebenundfünfzig\“ <126,127>. Damit endet das gemeinsame Unterrichtsgespräch und die Schüler und Schülerinnen arbeiten bis zum Ende der Unterrichtsstunde in Einzelarbeit.
Theoriereflexion
Die analysierte Unterrichtsszene zeigt ein kleinschrittiges Vorgehen auf, in dem an die Kinder kein besonders hoher fachlicher Anspruch gestellt wird. Es findet kein aktiv-entdeckendes Lernen statt, was gegebenenfalls auch nicht zielführend wäre, nimmt man an, dass es in dieser Szene in erster Linie um die Wiederholung und Vertiefung mathematischer Fach- und Symbolsprache im Bezug auf Zahlrelationen geht. Insofern rückt hier das sprachliche Lernen der Kinder in den Vordergrund der Betrachtung. Die Analyse zeigt, dass die Kinder keine auffälligen Probleme mit dem mathematischen Konzept der Zahlrelationen zu haben scheinen und ihnen die Bearbeitung derartiger Aufgaben keine fachlichen Schwierigkeiten bereiten. Auf der sprachlichen Ebene hingegen sieht dies anders aus. Somit besteht durchaus der Bedarf und auch das Potential anknüpfend an die mathematischen Fähigkeiten der Schüler und Schülerinnen Lernsituationen zu initiieren, in denen die Kinder explizit mit der mathematischen Fachsprache und Symbolsprache konfrontiert und in diese eingeführt werden (vgl. Pimm 1987). Dies scheint der Lehrperson bewusst zu sein, was sich unter anderem in ihrer an vielen Stellen gut ausgeprägten Rolle als sprachliches Vorbild zeigt. Allerdings verbleibt es dabei, dass die Lehrperson die Rolle des sprachlichen Vorbildes übernimmt, ohne dass sie Lernsituationen generiert, in denen die Kinder im Sinne der Zone der nächsten Entwicklung (vgl. Vygotzky 1969) diese sprachlichen Muster übernehmen können und an dieser Rolle selber wachsen können. In großen Teilen scheint der Unterricht so organisiert zu sein, dass viele Kinder, möglichst ohne Fehler zu machen, daran partizipieren können (vgl. Gersten et al 2009). Somit wird ebenfalls ein reibungsloser Verlauf - im Sinne eines interaktionalen Gleichflusses (vgl. Krummheuer & Brandt 2001) - garantiert, was die Spielräume der Kinder in dieser Szene sprachlich eigenständig produktiv zu werden und damit in ihrer sprachlichen Entwicklung voranzukommen einschränkt.
Das interpretative-rekonstruktive Vorgehen in fachdidaktischer Forschung erlaubt es nah an den empirischen Daten theoriegeleitet Phänomene des Lernens und Lehrens zu rekonstruieren. Diese Phänomene können in einem weiteren Schritt in bestehende Theorie eingeordnet und so erklärt werden bzw. über die Herausarbeitung von Inkonsistenzen mit bestehender Theorie zur Notwendigkeit von Theorieentwicklung führen. So wurde zu Beginn des Artikels auf theoretischer Ebene herausgearbeitet, in welchem Spannungsverhältnis sich der Mathematikunterricht und insbesondere das Mathematiklernen im inklusiven Unterricht befinden. Mathematiklernen lässt sich hiernach – in den in der Mathematikdidaktik vertretenen aktuellen Ansätzen - zum einen über offene Zugänge, eine gewisse Komplexität, einer intensiven sprachlichen Aushandlung, die in kollektiven Argumentation mündet und dem Anspruch mathematische Konzepte zu verstehen modellieren. Anderseits gibt es Zugänge – vielfach in sonderpädagogischen Ansätzen vertreten – die in Anbetracht geringerer kognitiver Leistungen einiger Kinder eine kleinschrittige Vermittlung von Fertigkeiten als das Ziel des Mathematiklernens proklamieren. Einigkeit zumindest einer Vielzahl von Untersuchungen scheint jedoch darüber zu bestehen, dass im Grundschulmathematikunterricht der sprachlichen Aushandlung und der gemeinsamen interaktiven Aushandlung der Gruppe eine besondere Bedeutung zukommt. Basierend auf dieser Annahme wurden zwei Unterrichtsszenen inklusiven Grundschulmathematikunterrichts analysiert, die unterschiedliche Zugänge und alltagspädagogische Vorstellungen zum Lernen von Mathematik der Lehrpersonen offenbarten. In den ausführlichen Analysen wurde rekonstruiert, dass der Unterricht der Lehrperson in der Szene „Gerade und ungerade Zahlen“ zwar den Versuch erkennen lässt, aktiv-entdeckend erkundete mathematisch anspruchsvolle Zusammenhänge gemeinsam im Unterrichtsdiskurs zu thematisieren hierbei jedoch durch eine starke kleinschrittige Lenkung der Lehrperson sich die mathematische Kommunikation und Argumentation der Schüler und Schülerinnen nicht optimal entwickeln kann. Des Weiteren ergeben sich in der analysierten Szene durch die offenen Fragestellungen der Lehrperson viele Sprachanlässe, die jedoch aufgrund der starken Engführung bzw. Nichtkoordinierung der Deutung der Lernenden durch die Lehrperson nicht in kollektive Argumentationen münden. Im Unterricht der Lehrperson in der Szene „Größer-Kleiner“ scheint der mathematisch Anspruch von Beginn an stark reduziert, was gegebenenfalls die Möglichkeit böte bildungssprachliche Anteile als Lerngegenstand in den Vordergrund zu rücken. Der Lehrperson gelingt es hier allerdings nicht die Kinder auf eine höhere Stufe eigener sprachlicher produktiven Teilnahme zu begleiten.
Als Resümee scheint erkennbar, dass in beiden Szenen Ansätze zur Umsetzung eines neueren Bildes von Mathematik erkennbar sind, was sich im Sinne der Qualitativen Induktion als ein einordnen in bestehende Theorie verstehen ließe. Erstere an ihrer starken Lenkung des Unterrichts zu scheitern scheint und Letztere an der mangelnden anspruchsvollen Einbindung der Kinder durch die Lehrperson. Es emergieren so keine interaktionalen Verdichtungen (vgl. Krummheuer & Brandt 2001) in denen optimierte Bedingungen für das Lernen von mathematische Konzepte und oder sprachliche Strukturen entstehen. Hier scheint weiterer Forschungsbedarf gegeben, um zu rekonstruieren, inwiefern sich diese Einzelfallphänomene über Komparation auf eine breitere empirische Basis stellen lassen würden und welche gemeinsamen Strukturen sich eventuell oberhalb dieser vordergründig unterschiedlichen Gründe des Scheiterns einer Umsetzung des neuen Bildes von Mathematik herauskristallisieren lassen.
Als erste vorsichtige Implikationen für die Praxis des Lehren und Lernens in inklusiven Unterrichtssettings könnte ein Schlüssel zur Verbesserung der Möglichkeiten für das gleichzeitige Lernen von sprachlich und fachlichen Inhalten neben der Entwicklung von förderlichen Lernumgebungen über eine Ausweitung der Interpretationskompetenz der Lehrperson erfolgen, so dass diese auch auf der Ebene der situativen kommunikativen Aushandlung im Unterricht das „neue“ Bild von Mathematik überliefern können. Zusammenfassend lässt sich festhalten, dass intensiver Klärungsbedarf darüber zu bestehen scheint, wie inklusives Lernen im Fach Mathematik in Schulen umzusetzen ist, um wirklich allen Kindern gerecht werden zu können. Es bedarf weitergehender Analyse, die sich mit den Bedingungen fachlicher und sozialer Teilhabe aller Kinder in einem inklusiven Mathematikunterricht beschäftigen. Hierfür muss unter anderem auch die Frage nach einer Methode zur Bestimmung von fachlicher und sozialer Teilhabe geklärt werden.
[1] Bis zu Beginn der 2000er Jahre ließen sich Forschungsbemühungen in diesem mathematikdidaktischen Feld unter dem Begriff Interpretative Unterrichtsforschung subsumieren. Durch die verstärkte Betrachtung außerschulischen Lernens in jüngsten Forschungsansätzen erscheint die Bezeichnung nicht mehr zeitgemäß (vgl. z.B. Tiedemann 2012, Brandt, Vogel & Krummheuer 2011, Schütte 2014). Insofern sprechen wir im Weiteren von Interpretativer Forschung.
[2] Vgl. „grand theories“ (Merton 1968, S. 50 f.) und „definitive concepts“ (Blumer 1954, S. 7).
[3] Vgl. „middle range theories“ (Merton 1968, S. 50 f.) und „sensitizing concepts“ (Blumer 1954, S. 7).
[4] Der Genetische Individualismus steht in der Tradition des ‚späten‘ Piaget und Kohlberg (vgl. Miller 1986, S. 15 ff.).
[5] Der Genetische Interaktionismus geht auf Grundannahmen soziologischer und psychologischer Arbeiten zurück wie z. B. denen von Durkheim, Mead, dem ‚frühen‘ Piaget und Vygotski. In diesen Arbeiten wird die soziale Kooperation oder soziale Interaktion als grundlegend für Lernprozesse des Individuums angesehen (vgl. Miller 1986, S. 15 ff.).
[6] Es kann hier leider nur ein Teil der wichtigsten Autorinnen und Autoren genannt werden.
[7] Die Verwendung dieses Begriffes bedeutet keineswegs, dass davon ausgegangen wird, hiermit könne man eine in sich homogone Gruppe benennen und sie soll nicht zu einer Verengung des Inklusionsbegriffs auf die Integration von Kindern mit sonderpädagogischem Förderbedarf führen.